题目内容
13. 如图所示,摩托车做腾跃特级表演,以初速度v0冲上高为h、顶部水平的高台,然后从高台水平飞出,若摩托车始终以额定功率P行驶,经时间t从坡底到达坡顶,人和车的总质量为m,且各种阻力的影响可忽略不计,求:
如图所示,摩托车做腾跃特级表演,以初速度v0冲上高为h、顶部水平的高台,然后从高台水平飞出,若摩托车始终以额定功率P行驶,经时间t从坡底到达坡顶,人和车的总质量为m,且各种阻力的影响可忽略不计,求:(1)人和车到达坡顶时的速度v
(2)人和车飞出的水平距离x
(3)当h为多少时,人和车飞出的水平距离最远,并求出最大值Xmax.
分析 (1)根据动能定理,抓住功率不变求出人和车到达坡顶时的速度大小.
(2)根据高度求出平抛运动的时间,结合初速度和时间求出水平位移.
(3)运用数学知识:不等式$\sqrt{ab}≤\frac{a+b}{2}$,当a=b时取等号,对水平方向距离来确定h取何值时,s有最大值.
解答 解:(1)根据动能定理得:Pt-mgh=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$,
解得:v=$\sqrt{\frac{2Pt-2mgh+m{{v}_{0}}^{2}}{m}}$.
(2)根据h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}$,则水平距离为:x=vt=$\sqrt{\frac{(2Pt-2mgh+m{{v}_{0}}^{2})•2h}{mg}}$.
(3)x=vt=$\sqrt{\frac{(2Pt-2mgh+m{{v}_{0}}^{2})•2h}{mg}}$=$\sqrt{2h(\frac{{{v}_{0}}^{2}}{g}+\frac{2Pt}{mg}-2h)}$.
利用不等式$\sqrt{ab}≤\frac{a+b}{2}$当a=b时取等号,所以由上式可得:
当$2h=\frac{{{v}_{0}}^{2}}{g}+\frac{2Pt}{mg}-2h$时,
即$h=\frac{1}{4}(\frac{{{v}_{0}}^{2}}{g}+\frac{2Pt}{mg})$时,x取最大值,xmax=2h.
答:(1)人和车到达坡顶时的速度v为$\sqrt{\frac{2Pt-2mgh+m{{v}_{0}}^{2}}{m}}$.
(2)人和车飞出的水平距离x为$\sqrt{\frac{(2Pt-2mgh+m{{v}_{0}}^{2})•2h}{mg}}$.
(3)当$h=\frac{1}{4}(\frac{{{v}_{0}}^{2}}{g}+\frac{2Pt}{mg})$时,人和车飞出的水平距离最远,最大值Xmax为2h.
点评 本题考查动能定理和平抛运动的规律,难度不大,关键是利用好数学知识求的极值.

| A. | 物体对斜面的压力和斜面对物体的支持力均属于弹力 | |
| B. | 物体对斜面的摩擦力和斜面对物体的摩擦力是一对平衡力 | |
| C. | 物体所受重力和斜面对物体的作用力是平衡力 | |
| D. | 物体所受重力可以分解为沿斜面向下的力和对斜面的压力 |
| A. | 电容器是一种储存电荷的装置 | B. | 避雷针是用来防止静电的 | ||
| C. | 电感器应用了电流的热效应 | D. | 电磁炉应用了电磁感应现象 |
 两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )
两个轻弹簧分别与质量为m的物体相连接,劲度系数分别为k1和k2,装置呈竖直状态静止在水平地面上,如图所示.劲度系数为k2的弹簧与地面不栓接.现用竖直向上的拉力F拉劲度系数为k1的弹簧上端A点,使A点缓慢上升,当下边弹簧的下端即将离开地面时( )| A. | 物体比施加F前高$\frac{mg}{{k}_{2}}$ | B. | A点比施加F前高$\frac{mg}{{k}_{1}}$ | ||
| C. | F<mg | D. | F>mg |
| A. | 法拉第发现了电流的磁效应. | |
| B. | 库仑提出了库仑定律,并最早用实验测得元电荷e的数值 | |
| C. | 伽利略发现了行星运动的规律,并通过实验测出了引力常量 | |
| D. | 荷兰科学家昂尼斯(或昂纳斯)发现大多数金属在温度降到某一值时,都会出现电阻突然降为零的现象--超导现象 |
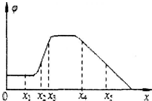
| A. | 空间各点场强的方向均与x轴垂直 | |
| B. | 电荷沿x轴从0移到x1的过程中,一定不受电场力的作用 | |
| C. | 正电荷沿x轴从x2移到x3的过程中,电场力做正功 | |
| D. | 负电荷沿x轴从x4移到x5的过程中,电场力做负功 |
 如图所示.将两质量均为5kg的相同木块A、B至于粗糙水平地面上,中间用一轻弹簧连接,两木块与水平地面之间的动摩擦因数均为0.2,夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m,现用水平向左的推力F作用在木块B上,在该力从零开始逐渐增大的过程中AB及弹簧始终保持静止状态,(取g=10m/s2,最大静摩擦力等于滑动摩擦力)下列说法正确的是( )
如图所示.将两质量均为5kg的相同木块A、B至于粗糙水平地面上,中间用一轻弹簧连接,两木块与水平地面之间的动摩擦因数均为0.2,夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m,现用水平向左的推力F作用在木块B上,在该力从零开始逐渐增大的过程中AB及弹簧始终保持静止状态,(取g=10m/s2,最大静摩擦力等于滑动摩擦力)下列说法正确的是( )| A. | 木块A所受摩擦力大小始终为10N | B. | 力F最大值为10N | ||
| C. | 木块B所受摩擦力逐渐变小 | D. | 木块B所受摩擦力先变小然后变大 |
 一列横波沿x轴传播,传播方向未知.t时刻与t+0.4s时刻波形相同,两时刻在x轴上-3m~3m的区间内的波形如图所示.由图象可以判定
一列横波沿x轴传播,传播方向未知.t时刻与t+0.4s时刻波形相同,两时刻在x轴上-3m~3m的区间内的波形如图所示.由图象可以判定