题目内容
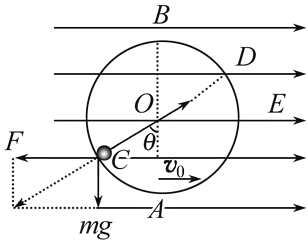
【题目】如图所示，在竖直平面内固定的圆形绝缘轨道的圆心为
、半径为
、内壁光滑，
、
两点分别是圆轨道的最低点和最高点。该区间存在方向水平向右的匀强电场，一质量为
的带电小球(可视为质点)恰好能静止在
点。若在点给小球一个初速度使它在轨道内侧恰好能做完整的圆周运动（小球的电荷量不变）。已知、、
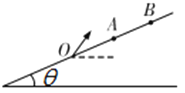
在同一直线上，它们的连线与竖直方向的夹角
，重力加速度为
。求：
(1)小球所受的电场力
的大小；
(2)小球做圆周运动，在点的速度大小及在点对轨道压力的大小。
【答案】(1)
；(2)9mg
【解析】
(1)小球在C点静止，受力如图所示
由平衡条件得
F＝mgtan60°①
解得：
F＝
mg②
(2)小球在轨道内侧恰好做完整的圆周运动，在D点小球速度最小，对轨道的压力为零，则
③
解得小球在D点的速度
vD＝
④
小球由轨道上A点运动到D点的过程，根据动能定理得
⑤
解得小球在A点的速度
vA＝2⑥
小球在A点，根据牛顿第二定律得：
⑦
解得：
⑧
根据牛顿第三定律得：小球对轨道的压力大小为
练习册系列答案
相关题目
