题目内容
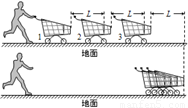
如图所示,静置于水平地面的三辆手推车沿一直线排列,质量均为m,人在极短时间内给第一辆车一水平冲量使其运动,当车运动了距离L时与第二辆车相碰,两车以共同速度继续运动了距离L时与第三车相碰,三车以共同速度又运动了距离L时停止.车运动时受到的摩擦阻力恒为车所受重力的k倍,重力加速度为g,若车与车之间仅在碰撞时发生相互作用,碰撞时间很短,忽略空气阻力,求:(1)整个过程中摩擦阻力所做的总功;
(2)人给第一辆车水平冲量的大小;
(3)第一次与第二次碰撞系统功能损失之比.
【答案】分析:(1)摩擦力大小为kmg,方向与运动方向相反,故由功的定义可知其做的总功;
(2)对三个减速过程和两个碰撞过程分别运用动能定理和动量守恒定律列式可求解;
(3)由于两次碰撞之前之后的速度已知,即可以求出第一次和第二次动能损失.
解答:解:(1)设运动过程中摩擦阻力做的总功为W,则W=-kmgL-2kmgL-3kmgL=-6kmgL;
即整个过程中摩擦阻力所做的总功为-6kmgL.
(2)设第一车初速度为u,第一次碰前速度为v1,碰后共同速度为u1;第二次碰前速度为v2,碰后共同速度为u2;人给第一车的水平冲量大小为I.
由动能定理,对三段减速过程列式
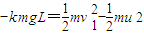
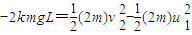
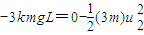
由动量守恒定律对两次碰撞过程列式
mv1=2mu1
2mv2=3mu2
人推车过程,由动量定理列式
I=mu-0
联立以上六式,解得:I=2m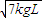
即人给第一辆车水平冲量的大小为2m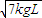 .
.
(3)设两次碰撞中系统动能损失分别为△Ek1和△Ek2
△Ek1= (2m)u12-
(2m)u12- mv12=
mv12=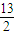 kmgL
kmgL
△Ek2═ (3m)u22-
(3m)u22- (2m)v22=
(2m)v22= kmgL
kmgL
因而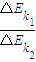 =
=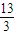
即第一次与第二次碰撞系统功能损失之比为13:3.
点评:本题关键在于运动的过程较多,有三个匀减速过程和两个碰撞过程,可以交叉运用动能定理和动量守恒定律列式求解,题中涉及的字母较多,要有足够的耐心,更要细心!
(2)对三个减速过程和两个碰撞过程分别运用动能定理和动量守恒定律列式可求解;
(3)由于两次碰撞之前之后的速度已知,即可以求出第一次和第二次动能损失.
解答:解:(1)设运动过程中摩擦阻力做的总功为W,则W=-kmgL-2kmgL-3kmgL=-6kmgL;
即整个过程中摩擦阻力所做的总功为-6kmgL.
(2)设第一车初速度为u,第一次碰前速度为v1,碰后共同速度为u1;第二次碰前速度为v2,碰后共同速度为u2;人给第一车的水平冲量大小为I.
由动能定理,对三段减速过程列式
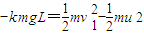
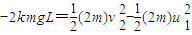
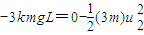
由动量守恒定律对两次碰撞过程列式
mv1=2mu1
2mv2=3mu2
人推车过程,由动量定理列式
I=mu-0
联立以上六式,解得:I=2m
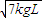
即人给第一辆车水平冲量的大小为2m
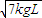 .
.(3)设两次碰撞中系统动能损失分别为△Ek1和△Ek2
△Ek1=
 (2m)u12-
(2m)u12- mv12=
mv12=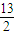 kmgL
kmgL△Ek2═
 (3m)u22-
(3m)u22- (2m)v22=
(2m)v22= kmgL
kmgL因而
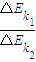 =
=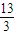
即第一次与第二次碰撞系统功能损失之比为13:3.
点评:本题关键在于运动的过程较多,有三个匀减速过程和两个碰撞过程,可以交叉运用动能定理和动量守恒定律列式求解,题中涉及的字母较多,要有足够的耐心,更要细心!

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 如图所示,静置于水平地面的三辆手推车沿一直线排列,质量均为m,人在极短时间内给第一辆车一水平冲量使其运动,当车运动了距离L时与第二辆车相碰,两车以共同速度继续运动了距离L时与第三车相碰,三车以共同速度又运动了距离L时停止.车运动时受到的摩擦阻力恒为车所受重力的k倍,重力加速度为g,若车与车之间仅在碰撞时发生相互作用,碰撞时间很短,忽略空气阻力,求:
如图所示,静置于水平地面的三辆手推车沿一直线排列,质量均为m,人在极短时间内给第一辆车一水平冲量使其运动,当车运动了距离L时与第二辆车相碰,两车以共同速度继续运动了距离L时与第三车相碰,三车以共同速度又运动了距离L时停止.车运动时受到的摩擦阻力恒为车所受重力的k倍,重力加速度为g,若车与车之间仅在碰撞时发生相互作用,碰撞时间很短,忽略空气阻力,求:


