题目内容
 在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,O为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=
在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,O为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=
| ||
| 3 |
(1)求半圆柱形透明物体的折射率.
(2)若用一束平行于AO的水平光线从D点射到半圆柱形透明物体上,折射入半圆柱体后再从竖直表面射出,如图所示.已知入射光线与AO的距离为
| ||
| 2 |
分析:(1)甲刚好看到不乙,是因乙发出的光线在B点恰好发生了全反射,入射角等于临界角,作出光路图,由光的折射定律可求得折射率
(2)当光从图示位置射入,经过二次折射后射出球体,由折射定律可求出射出光线的出射角θ.
(2)当光从图示位置射入,经过二次折射后射出球体,由折射定律可求出射出光线的出射角θ.
解答:解:(1)如下图所示.设∠OBC=θ,透明物体的折射率为n,由题意,甲刚好看到不乙,是因乙发出的光线 在B点恰好发生了全反射,则θ等于临界角.
在B点恰好发生了全反射,则θ等于临界角.
因sinθ=
=
,
又由全反射临界角公式:sinθ=
,
解得:n=
.
(2)设入射光线与1/4球体的交点为D,连接OD,OD即 为入射点的法线.因此,图中的角a为入射角.过D点作水平表面的垂线,垂足为E.依题意,∠ODE=α.又由△ODE知:sinα=
为入射点的法线.因此,图中的角a为入射角.过D点作水平表面的垂线,垂足为E.依题意,∠ODE=α.又由△ODE知:sinα=
…①
设光线在D点的折射角为β,由折射定律得:
=
… ②
由①②式得:β=30°… ③
由几何关系知,光线在竖直表面上的入射角γ为30°.由折射定律得:
=
…④
因此sinθ=
解得:θ=60°
答:(1)半圆柱形透明物体的折射率为
.
(2)出射角θ为60°.
 在B点恰好发生了全反射,则θ等于临界角.
在B点恰好发生了全反射,则θ等于临界角.因sinθ=
| OC |
| R |
| ||
| 3 |
又由全反射临界角公式:sinθ=
| 1 |
| n |
解得:n=
| 3 |
(2)设入射光线与1/4球体的交点为D,连接OD,OD即
 为入射点的法线.因此,图中的角a为入射角.过D点作水平表面的垂线,垂足为E.依题意,∠ODE=α.又由△ODE知:sinα=
为入射点的法线.因此,图中的角a为入射角.过D点作水平表面的垂线,垂足为E.依题意,∠ODE=α.又由△ODE知:sinα=
| ||
| 2 |
设光线在D点的折射角为β,由折射定律得:
| sinα |
| sinβ |
| 3 |
由①②式得:β=30°… ③
由几何关系知,光线在竖直表面上的入射角γ为30°.由折射定律得:
| sinr |
| sinθ |
| 1 | ||
|
因此sinθ=
| ||
| 2 |
解得:θ=60°
答:(1)半圆柱形透明物体的折射率为
| 3 |
(2)出射角θ为60°.
点评:光的折射是3-4模块中的重点内容,考试热点,本题关键要理解甲乙看不到对方的原因,并能熟练应用光的折射定律.

练习册系列答案
相关题目
 A.(选修模块3-3)
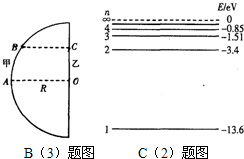
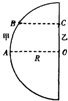
A.(选修模块3-3)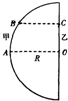 (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?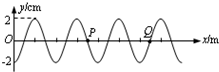

 A.(选修模块3-3)
A.(选修模块3-3) D3,则在该状态下体积为V的二氧化碳气体变成固体后体积为多少?
D3,则在该状态下体积为V的二氧化碳气体变成固体后体积为多少? (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少? →
→ .若
.若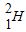 和
和 迎面碰撞,初速度大小分别为v1、v2,
迎面碰撞,初速度大小分别为v1、v2, 、
、 、
、 He、
He、 的质量分别为m1、m2、m3、m4,反应后
的质量分别为m1、m2、m3、m4,反应后 He的速度大小为v3,方向与
He的速度大小为v3,方向与 的运动方向相同,求中子
的运动方向相同,求中子 的速度
的速度