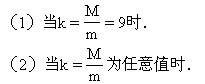题目内容
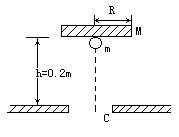
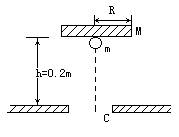
质量为M的圆薄板与质量为m的小球用轻绳连接，开始时板与球紧挨，在它们正下方h=0.2m处有一固定支架C，支架上有一半径为R′的圆孔，圆孔直径小于圆薄板的直径，圆板中心和圆孔中心在同一竖直线上，如图所示．让薄板与小球同时自由下落，圆薄板与C孔发生弹性碰撞（没有机械能损失），圆板M与孔C发生第一次碰撞后分离，直到轻绳第一次绷紧，为使轻绳第一次绷紧时，板与球的共同速度v共方向竖直向下，求在下列条件下轻绳长度应满足的条件：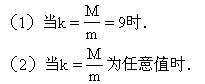
答案：见详解
解析：
提示：
解析：
| 本题有如下几个重要过程：
（1）M、m做自由落体运动，机械能守恒． （2）圆板M与孔C碰后，M、m分别以大小相等的初速度，向上做竖直上抛运动和向下的竖直下抛运动．由于重力Mg、mg的冲量作用，使圆板向上的动量MVm不断减小，小球向下的动量mvm不断增大． （3）随着时间的延续，圆板与小球的总动量可以由方向向上演变成方向向下，此时小球向下的动量应大于圆板向上的动量，用此关系可求出所需要的时间．然后用运动学位移公式可求出绳的最小长度．
代入（5），得L1=2v0t=0.64m由（6）（7）可得绳的最大长度L2应满足
则绳长L应为0.64m＜L＜1.6m
|
提示：
| 考查动量定理。 |
练习册系列答案
相关题目
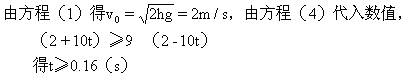
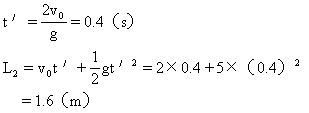
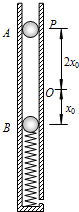质量为m的小球B与质量为2m的小球C之间用一根轻质弹簧连接，现把它们放置在竖直固定的内壁光滑的直圆筒内，平衡时弹簧的压缩量为x0，如图所示，设弹簧的弹性势能与弹簧的形变量（即伸长量或缩短量）的平方成正比．小球A从小球B的正上方距离为3x0的P处自由落下，落在小球B上立刻与小球B粘连在一起向下运动，它们到达最低点后又向上运动．已知小球A的质量也为m时，它们恰能回到O点（设3个小球直径相等，且远小于x0，略小于直圆筒内径），问小球A至少在B球正上方多少距离处自由落下，与B球粘连后一起运动，可带动小球C离开筒底．
质量为m的A球与质量为M的B球，分别连接在轻质弹簧的两端，如图所示，B球用平行于斜面的细线固定在倾角为30°的光滑斜面上，A、B球处于静止状态，当细线被剪断的瞬间，A、B两球的加速度大小分别为（ ）
如图所示，BCPC′D是螺旋轨道，半径为R的圆O与半径为2R的BCD圆弧相切于最低点C，与水平面夹角都是37°的倾斜轨道AB、ED分别与BC、C′D圆弧相切于B、D点（C、C′均为竖直圆的最底点），将一劲度系数为k的轻质弹簧的一端固定在AB轨道的有孔固定板上，平行于斜面的细线穿过有孔固定板和弹簧跨过定滑轮将小球和大球连接，小球与弹簧接触但不相连，小球质量为m，大球质量为
