题目内容
1951年,物理学家发现了“电子偶数”,所谓“电子偶数”就是由一个负电子和一个正电子绕它们的质量中心旋转形成的相对稳定的系统,已知正负电子的质量均为m,普朗克常数为h,假设“电子偶数”中正、负电子绕它们质量中心做匀速圆周运动的轨道半径为r,运动速度为v及电子的质量满足量子化理论:2mevern=| nh |
| 2π |
| e2 |
| L |
分析:电子偶数能量等于两个电子动能和电势能之和,库仑引力提供向心力,根据牛顿第二定律求出电子的动能,结合电势能表达式和2mvnrn=n
,求出电子偶数的能量.
| h |
| 2π |
解答:解:电子绕质量中心转动,库仑力提供向心力有:k
=m
,其中L=2r
故:k
=mv2r,根据2mevern=
(2π),n=1,2…
上两式相比得:v=
,代入下式中,
E=
mv2×2-k
=mv2-2mv2=-mv2
所以E=-m(
)2,所以E1=-
;
答:n=1时“电子偶数”的能量为-
.
| e2 |
| L2 |
| v2 |
| r |
故:k
| e2 |
| 4 |
| nh |
| 2π |
上两式相比得:v=
| ke2π |
| nh |
E=
| 1 |
| 2 |
| e2 |
| L |
所以E=-m(
| ke2π |
| nh |
| mk2e4π2 |
| h2 |
答:n=1时“电子偶数”的能量为-
| mk2e4π2 |
| h2 |
点评:考查电子受到的电场力作用为向心力做匀速圆周运动,掌握牛顿第二定律的应用,知道系统的能量是动能与电势能之和.

练习册系列答案
相关题目
 ,n=1,2…,“电子偶数”的能量为正负电子运动的动能和系统的电势能之和,已知两正负电子相距为L时的电势能为
,n=1,2…,“电子偶数”的能量为正负电子运动的动能和系统的电势能之和,已知两正负电子相距为L时的电势能为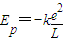 .试求n=1时“电子偶数”的能量.
.试求n=1时“电子偶数”的能量.