题目内容
 (2010?洛阳模拟)如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电量为+q,质量为m(不计重力),从点P经电场加速后,从小孔 Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为a=45°,孔Q到板的下端C的距离为L.当M、N两板间电压取最大值时,粒子恰垂直打在CD板上.求:
(2010?洛阳模拟)如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到某一最大值之间的各种数值.静止的带电粒子带电量为+q,质量为m(不计重力),从点P经电场加速后,从小孔 Q进入N板右侧的匀强磁场区域,磁感应强度大小为B,方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为a=45°,孔Q到板的下端C的距离为L.当M、N两板间电压取最大值时,粒子恰垂直打在CD板上.求:(1)两板间电压的最大值Um;
(2)CD板上可能被粒子打中的区域的长度x;
(3)粒子在磁场中运动的最长时间tm.
分析:(1)粒子恰好垂直打在CD板上,根据粒子的运动的轨迹,可以求得粒子运动的半径,由半径公式可以求得电压的大小;
(2)当粒子的运动的轨迹恰好与CD板相切时,这是粒子能达到的最下边的边缘,在由几何关系可以求得被粒子打中的区域的长度.
(3)打在QE间的粒子在磁场中运动的时间最长,均为半周期,根据周期公式即可求解.
(2)当粒子的运动的轨迹恰好与CD板相切时,这是粒子能达到的最下边的边缘,在由几何关系可以求得被粒子打中的区域的长度.
(3)打在QE间的粒子在磁场中运动的时间最长,均为半周期,根据周期公式即可求解.
解答: 解:(1)M、N两板间电压取最大值时,粒子恰垂直打在CD板上,
解:(1)M、N两板间电压取最大值时,粒子恰垂直打在CD板上,
所以圆心在C点,CH=QC=L,故半径R1=L
又因qvB=m
qUm=
mv12
所以Um=
(2)设轨迹与CD板相切于K点,半径为R2,在△AKC中:
sin45°=
所以R2=(
-1)L
即KC长等于R2=(
-1)L
所以CD板上可能被粒子打中的区域即为HK的长度,
x=HK=R1-R2=L-(
-1)L=(2-
)L
(3)打在QE间的粒子在磁场中运动的时间最长,均为半周期:
T=
所以tm=
T=
答:(1)两板间电压的最大值Um为
;
(2)CD板上可能被粒子打中的区域的长度x为(2-
)L;
(3)粒子在磁场中运动的最长时间tm为
.
 解:(1)M、N两板间电压取最大值时,粒子恰垂直打在CD板上,
解:(1)M、N两板间电压取最大值时,粒子恰垂直打在CD板上,所以圆心在C点,CH=QC=L,故半径R1=L
又因qvB=m
| v12 |
| R1 |
qUm=
| 1 |
| 2 |
所以Um=
| qB2L2 |
| 2m |
(2)设轨迹与CD板相切于K点,半径为R2,在△AKC中:
sin45°=
| R2 |
| L-R2 |
所以R2=(
| 2 |
即KC长等于R2=(
| 2 |
所以CD板上可能被粒子打中的区域即为HK的长度,
x=HK=R1-R2=L-(
| 2 |
| 2 |
(3)打在QE间的粒子在磁场中运动的时间最长,均为半周期:
T=
| 2πm |
| qB |
所以tm=
| 1 |
| 2 |
| πm |
| qB |
答:(1)两板间电压的最大值Um为
| qB2L2 |
| 2m |
(2)CD板上可能被粒子打中的区域的长度x为(2-
| 2 |
(3)粒子在磁场中运动的最长时间tm为
| πm |
| qB |
点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
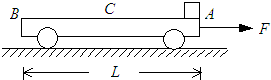 (2010?洛阳模拟)如图所示,光滑水平地面上停着一辆平板车,其质量为2m,长为L,车上右端(A点)有一块静止的质量为m的小金属块.金属块与平板车的上表面之间存在摩擦,以上表面的中点C为分界点,已知金属块与AC段间的动摩擦因数为μ,与CB段的动摩擦因数为未知.现给车一个向右的水平恒力F=5μmg,使车向右运动,同时金属块在车上也开始滑动,当金属块滑到中点C时,立即撤去这个水平恒力F,最后金属块恰好停在车的左端(B点).已知重力加速度为g,求:
(2010?洛阳模拟)如图所示,光滑水平地面上停着一辆平板车,其质量为2m,长为L,车上右端(A点)有一块静止的质量为m的小金属块.金属块与平板车的上表面之间存在摩擦,以上表面的中点C为分界点,已知金属块与AC段间的动摩擦因数为μ,与CB段的动摩擦因数为未知.现给车一个向右的水平恒力F=5μmg,使车向右运动,同时金属块在车上也开始滑动,当金属块滑到中点C时,立即撤去这个水平恒力F,最后金属块恰好停在车的左端(B点).已知重力加速度为g,求:
 (2010?洛阳模拟)据报道,我国将于2011年上半年发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并与“天宫一号”实现对接.某同学得知上述消息后,画出“天宫一号”和“神舟八号”绕地球做匀速圆周运动的假想图如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由此假想图,下列判断正确的是( )
(2010?洛阳模拟)据报道,我国将于2011年上半年发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并与“天宫一号”实现对接.某同学得知上述消息后,画出“天宫一号”和“神舟八号”绕地球做匀速圆周运动的假想图如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由此假想图,下列判断正确的是( ) (2010?洛阳模拟)如图所示为氢原子的能级图.当氢原子从n=4的能级跃迁到n=2的能级时,辐射出光子a;当氢原子从n=3的能级跃迁到n=l的能级时,辐射出光子b.则下列判断正确的是( )
(2010?洛阳模拟)如图所示为氢原子的能级图.当氢原子从n=4的能级跃迁到n=2的能级时,辐射出光子a;当氢原子从n=3的能级跃迁到n=l的能级时,辐射出光子b.则下列判断正确的是( ) (2010?洛阳模拟)水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ,现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图所示,在θ从0°逐渐增大到90°的过程中,木箱的速度保持不变,则( )
(2010?洛阳模拟)水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ,现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图所示,在θ从0°逐渐增大到90°的过程中,木箱的速度保持不变,则( )