题目内容
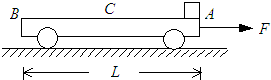 (2010?洛阳模拟)如图所示,光滑水平地面上停着一辆平板车,其质量为2m,长为L,车上右端(A点)有一块静止的质量为m的小金属块.金属块与平板车的上表面之间存在摩擦,以上表面的中点C为分界点,已知金属块与AC段间的动摩擦因数为μ,与CB段的动摩擦因数为未知.现给车一个向右的水平恒力F=5μmg,使车向右运动,同时金属块在车上也开始滑动,当金属块滑到中点C时,立即撤去这个水平恒力F,最后金属块恰好停在车的左端(B点).已知重力加速度为g,求:
(2010?洛阳模拟)如图所示,光滑水平地面上停着一辆平板车,其质量为2m,长为L,车上右端(A点)有一块静止的质量为m的小金属块.金属块与平板车的上表面之间存在摩擦,以上表面的中点C为分界点,已知金属块与AC段间的动摩擦因数为μ,与CB段的动摩擦因数为未知.现给车一个向右的水平恒力F=5μmg,使车向右运动,同时金属块在车上也开始滑动,当金属块滑到中点C时,立即撤去这个水平恒力F,最后金属块恰好停在车的左端(B点).已知重力加速度为g,求:(1)撤去力F的瞬间,金属块的速度v1、车的速度v2分别为多少?
(2)金属块与CB段的动摩擦因数μ′.
分析:(1)撤去F前,根据牛顿第二定律和运动学公式求解
(2)撤去F后,金属块在平板车的CB段滑动的过程,根据动量守恒和能量守解答
(2)撤去F后,金属块在平板车的CB段滑动的过程,根据动量守恒和能量守解答
解答:解:(1)撤去F前,根据牛顿第二定律,有:
金属块:μmg=ma1
平板车:5μmg-μmg=2ma2
从给车一个向右的水平恒力到刚撤去该力的过程,平板车与金属块发生的位移满足关系:s2-s1=
L
即:
a2t2-
a1t2=
解得:t=
所以:v1=a1t=
v2=a2t=2
(2)撤去F后,金属块在平板车的CB段滑动的过程,设最终的共同速度为v3,
根据动量守恒,有:mv1+2mv2=3mv3
该过程系统机械能损失等于摩擦生热,有:
μ′mg?
=
m
+
?2m
-
?3m
解得:μ′=
μ
答:(1)撤去力F的瞬间,金属块的速度v1、车的速度v2分别为
,2
(2)金属块与CB段的动摩擦因数μ′=
μ.
金属块:μmg=ma1
平板车:5μmg-μmg=2ma2
从给车一个向右的水平恒力到刚撤去该力的过程,平板车与金属块发生的位移满足关系:s2-s1=
| 1 |
| 2 |
即:
| 1 |
| 2 |
| 1 |
| 2 |
| L |
| 2 |
解得:t=
|
所以:v1=a1t=
| μgL |
v2=a2t=2
| μgL |
(2)撤去F后,金属块在平板车的CB段滑动的过程,设最终的共同速度为v3,
根据动量守恒,有:mv1+2mv2=3mv3
该过程系统机械能损失等于摩擦生热,有:
μ′mg?
| L |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
解得:μ′=
| 2 |
| 3 |
答:(1)撤去力F的瞬间,金属块的速度v1、车的速度v2分别为
| μgL |
| μgL |
(2)金属块与CB段的动摩擦因数μ′=
| 2 |
| 3 |
点评:本题关键要抓住金属块和车运动的时间相同,末速度与加速度成正比,写出平板车的加速度.金属块与平板车的相对位移与摩擦生热有关,运用能量守恒是常用的思路.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目

 (2010?洛阳模拟)据报道,我国将于2011年上半年发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并与“天宫一号”实现对接.某同学得知上述消息后,画出“天宫一号”和“神舟八号”绕地球做匀速圆周运动的假想图如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由此假想图,下列判断正确的是( )
(2010?洛阳模拟)据报道,我国将于2011年上半年发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并与“天宫一号”实现对接.某同学得知上述消息后,画出“天宫一号”和“神舟八号”绕地球做匀速圆周运动的假想图如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由此假想图,下列判断正确的是( ) (2010?洛阳模拟)如图所示为氢原子的能级图.当氢原子从n=4的能级跃迁到n=2的能级时,辐射出光子a;当氢原子从n=3的能级跃迁到n=l的能级时,辐射出光子b.则下列判断正确的是( )
(2010?洛阳模拟)如图所示为氢原子的能级图.当氢原子从n=4的能级跃迁到n=2的能级时,辐射出光子a;当氢原子从n=3的能级跃迁到n=l的能级时,辐射出光子b.则下列判断正确的是( ) (2010?洛阳模拟)水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ,现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图所示,在θ从0°逐渐增大到90°的过程中,木箱的速度保持不变,则( )
(2010?洛阳模拟)水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ,现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图所示,在θ从0°逐渐增大到90°的过程中,木箱的速度保持不变,则( )