题目内容
13. 如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙壁.重物质量为木板质量的两倍,重物与木板间的动摩擦因数为?.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙壁碰撞到再次与重物速度相同时,木板右端离墙壁的距离.
如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙壁.重物质量为木板质量的两倍,重物与木板间的动摩擦因数为?.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙壁碰撞到再次与重物速度相同时,木板右端离墙壁的距离.
分析 由动量守恒可明确碰后的速度,再由动量定理及牛顿第二定律结合运动学公式可求得木板右端离墙壁的距离.
解答 解:设木板质量为m,重物质量为2m,取向右为正方向,由动量守恒得:
2mv0-mv0=3mv
设从第一次与墙壁碰撞到重物和木板具有共同速度v所用时间为t,对木板由动量定理得:
2?mgt=mv-m(-v0)
对木板由牛顿第二定律得
-2?mg=ma
木板从第一次与墙壁碰撞到再次与重物速度相同时,木板右端离墙壁的距离为:
x=v0t+$s={v_0}t+\frac{1}{2}a{t^2}$
解得:x=$\frac{2{v}_{0}^{2}}{9μg}$
答:木板右端离墙壁的距离$\frac{2{v}_{0}^{2}}{9μg}$.
点评 本题是一道考查动量守恒和匀变速直线运动规律的过程复杂的好题,正确分析出运动规律是关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4. 如图,导线ab、cd跨接在电阻不计的光滑的导轨上,ab的电阻为2R,cd电阻为R.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
如图,导线ab、cd跨接在电阻不计的光滑的导轨上,ab的电阻为2R,cd电阻为R.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
 如图,导线ab、cd跨接在电阻不计的光滑的导轨上,ab的电阻为2R,cd电阻为R.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
如图,导线ab、cd跨接在电阻不计的光滑的导轨上,ab的电阻为2R,cd电阻为R.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )| A. | F1>F2 | B. | F1=F2 | C. | Uab>Ucd | D. | Uab=Ucd |
5.如图所示,匝数n=100匝、面积为S=0.448m2的导线框ABCD所在处的磁感应强度大小B=$\frac{\sqrt{2}}{10π}$T.线框绕垂直于磁场的轴OO′以角速度ω=100πrad/s匀速转动,并与理想升压变压器相连进行远距离输电,升压变压器的原副线圈匝数比为2:5,理想降压变压器副线圈接入一只“220V,1100W”的灯泡,且灯泡正常发光,输电线路总电阻r=20Ω,导线框及其余导线电阻不计,电表均为理想电表.则下列说法中正确的是( )

| A. | 电压表的读数为448V | |
| B. | 输电线路的电流为0.98A | |
| C. | 电流表的读数为2.5A | |
| D. | 降压变压器的原副线圈匝数比为5:1 |
3. 霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数).将传感器固定在霍尔元件上,沿z轴方向元件的厚度为d,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当元件沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向上的上、下表面的电势差U也不同,则( )
霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数).将传感器固定在霍尔元件上,沿z轴方向元件的厚度为d,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当元件沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向上的上、下表面的电势差U也不同,则( )
 霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数).将传感器固定在霍尔元件上,沿z轴方向元件的厚度为d,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当元件沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向上的上、下表面的电势差U也不同,则( )
霍尔式位移传感器的测量原理是:如图所示,有一个沿z轴方向的磁场,磁感应强度B=B0+kz(B0、k均为常数).将传感器固定在霍尔元件上,沿z轴方向元件的厚度为d,保持通过霍尔元件的电流I不变(方向如图中箭头所示).当元件沿z轴方向移动时,由于位置不同,霍尔元件在y轴方向上的上、下表面的电势差U也不同,则( )| A. | 若图中霍尔元件是电子导电,则下板电势高 | |
| B. | 磁感应强度B越大,上、下表面的电势差U越小 | |
| C. | 电流I取值越大,上、下表面的电势差U越小 | |
| D. | k越大,传感器灵敏度($\frac{△U}{△z}$)越高 |
 如图所示,水平转盘的中心处有一光滑的小孔,穿过小孔的细线一端与放在转盘上的物体A(视为质点)相连,另一端悬挂着物体B.已知物体A、B的质量相同,物体A到小孔的距离为r,且与水平转盘间的动摩擦因数为μ,其与水平转盘间的最大静摩擦力等于滑动摩擦力,重力加速度为g.现使水平转盘绕通过小孔的竖直轴匀速转动,问:转盘转动的角速度ω在什么范围内,物体A才能随转盘一起转动?
如图所示,水平转盘的中心处有一光滑的小孔,穿过小孔的细线一端与放在转盘上的物体A(视为质点)相连,另一端悬挂着物体B.已知物体A、B的质量相同,物体A到小孔的距离为r,且与水平转盘间的动摩擦因数为μ,其与水平转盘间的最大静摩擦力等于滑动摩擦力,重力加速度为g.现使水平转盘绕通过小孔的竖直轴匀速转动,问:转盘转动的角速度ω在什么范围内,物体A才能随转盘一起转动? 在“探究力的平行四边形定则”的实验中,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.
在“探究力的平行四边形定则”的实验中,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.

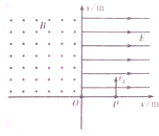 如图所示,在xoy平面内的第一象限内存在电场强度为E=2V/m,沿x轴正方向的匀强电场,在第二象限内存在磁感应强度B=1T、方向垂直xoy平面向外的匀强磁场,一个带负电的粒子,比荷为4C/kg,在x=3m处的P点以v0=4m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力,球:
如图所示,在xoy平面内的第一象限内存在电场强度为E=2V/m,沿x轴正方向的匀强电场,在第二象限内存在磁感应强度B=1T、方向垂直xoy平面向外的匀强磁场,一个带负电的粒子,比荷为4C/kg,在x=3m处的P点以v0=4m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力,球: