题目内容
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,t1时 ab边刚越过GH进入磁场Ⅰ区,此时线框恰好以速度 v1做匀速直线运动;t2时ab边下滑到JP与MN的中间位置,此时线框又恰好以速度v2做匀速直线运动。重力加速度为g,下列说法中正确的有:( )
| A.t1时,线框具有加速度a=3gsinθ |
| B.线框两次匀速直线运动的速度v1: v2=2:1 |
| C.从t1到t2过程中,线框克服安培力做功的大小等于重力势能的减少量 |
D.从t1到t2,有 机械能转化为电能 机械能转化为电能 |
D
解析试题分析:由题意, 时,线框做匀速直线运动,加速度为零.A正确.
时,线框做匀速直线运动,加速度为零.A正确. 时,安培力
时,安培力 ;
; 时,安培力
时,安培力 ,由两式比较得,
,由两式比较得, .故B错误.从
.故B错误.从 到
到 过程中,线框的重力势能和动能均减小,根据功能关系得知,框克服安培力做功的大小等于重力势能的减少量与动能减小量之和.故C错误.根据能量守恒定律得:从
过程中,线框的重力势能和动能均减小,根据功能关系得知,框克服安培力做功的大小等于重力势能的减少量与动能减小量之和.故C错误.根据能量守恒定律得:从 到
到 ,线框中产生的电能为
,线框中产生的电能为 .故D正确.
.故D正确.
故选D
考点:导体切割磁感线时的感应电动势;
点评:本题中线框出现两次平衡状态,由 推导安培力的表达式是关键,要注意t2时刻线框ab、cd都切割磁感线产生感应电动势,线框中总电动势为2BLv.
推导安培力的表达式是关键,要注意t2时刻线框ab、cd都切割磁感线产生感应电动势,线框中总电动势为2BLv.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
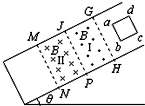 在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小均为B的强磁场区域,区域I的磁场方向垂直斜面向上,区域II的磁场方向垂直斜面向下,磁场和宽度HP及PN均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,t1时刻ab边刚越GH进入磁场I区域,此时导线框恰好以速度v1做匀速直线运动;t2时刻ab边下滑到JP与MN的中间位置,此时导线框又恰好以速度v2做匀速直线运动.重力加速度为g,下列说法中正确的是( )
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小均为B的强磁场区域,区域I的磁场方向垂直斜面向上,区域II的磁场方向垂直斜面向下,磁场和宽度HP及PN均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,t1时刻ab边刚越GH进入磁场I区域,此时导线框恰好以速度v1做匀速直线运动;t2时刻ab边下滑到JP与MN的中间位置,此时导线框又恰好以速度v2做匀速直线运动.重力加速度为g,下列说法中正确的是( )| A、当ab边刚越好JP时,导线框具有加速度大小为a=gsinθ | ||||
| B、导线框两次匀速直线运动的速度v1:v2=4:1 | ||||
| C、从t1到t2的过程中,导线框克服安培力做功的大小等于重力势能的减少 | ||||
D、从t1到t2的过程中,有
|
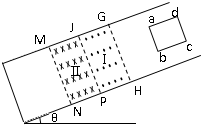 在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过GH进入磁场Ⅰ区时,恰好以速度 v1做匀速直线运动;当ab边下滑到JP与MN的中间位置时,线框又恰好以速度v2做匀速直线运动,从ab进入GH到MN与JP的中间位置的过程中,线框的动能变化量大小为△Ek,重力对线框做功的绝对值为W1,安培力对线框做功的绝对值为W2,下列说法中正确的有( )
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过GH进入磁场Ⅰ区时,恰好以速度 v1做匀速直线运动;当ab边下滑到JP与MN的中间位置时,线框又恰好以速度v2做匀速直线运动,从ab进入GH到MN与JP的中间位置的过程中,线框的动能变化量大小为△Ek,重力对线框做功的绝对值为W1,安培力对线框做功的绝对值为W2,下列说法中正确的有( )| A、v2=4v1 | B、v2=v1 | C、从ab进入GH到MN与JP的中间位置的过程中,机械能减小了W2 | D、从ab进入GH到MN与JP的中间位置的过程中,线框动能的变化量大小为△Ek=W2-W1. |
 在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过GH进入磁场Ⅰ区时,恰好以速度 v1做匀速直线运动;当ab边下滑到JP与MN的中间位置时,线框又恰好以速度v2做匀速直线运动,从ab进入GH到MN与JP的中间位置的过程中,线框的动能变化量为△Ek,重力对线框做功大小为W1,安培力对线框做功大小为W2,下列说法中正确的有( )
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过GH进入磁场Ⅰ区时,恰好以速度 v1做匀速直线运动;当ab边下滑到JP与MN的中间位置时,线框又恰好以速度v2做匀速直线运动,从ab进入GH到MN与JP的中间位置的过程中,线框的动能变化量为△Ek,重力对线框做功大小为W1,安培力对线框做功大小为W2,下列说法中正确的有( ) 在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过GH进入磁场Ⅰ区时,恰好以速度 v1做匀速直线运动;当ab边下滑到JP与MN的中间位置时,线框又恰好以速度v2做匀速直线运动,从ab进入GH到MN与JP的中间位置的过程中,线框的动能变化量大小为△Ek,重力对线框做功大小为W1,安培力对线框做功大小为W2,下列说法中正确的有( )
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过GH进入磁场Ⅰ区时,恰好以速度 v1做匀速直线运动;当ab边下滑到JP与MN的中间位置时,线框又恰好以速度v2做匀速直线运动,从ab进入GH到MN与JP的中间位置的过程中,线框的动能变化量大小为△Ek,重力对线框做功大小为W1,安培力对线框做功大小为W2,下列说法中正确的有( )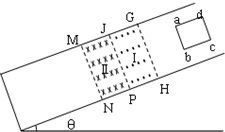 在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,t1时 ab边刚越过GH进入磁场Ⅰ区,此时线框恰好以速度 v1做匀速直线运动;t2时ab边下滑到JP与MN的中间位置,此时线框又恰好以速度v2做匀速直线运动.重力加速度为g,下列说法中正确的有( )
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,t1时 ab边刚越过GH进入磁场Ⅰ区,此时线框恰好以速度 v1做匀速直线运动;t2时ab边下滑到JP与MN的中间位置,此时线框又恰好以速度v2做匀速直线运动.重力加速度为g,下列说法中正确的有( )