题目内容
14. 如图所示木杆长5m,上端固定在某一点,由静止放开后让它自由落下(不计空气阻力),木杆通过悬点正下方20m处圆筒AB,圆筒AB长为5m,求:
如图所示木杆长5m,上端固定在某一点,由静止放开后让它自由落下(不计空气阻力),木杆通过悬点正下方20m处圆筒AB,圆筒AB长为5m,求:(1)木杆经过圆筒的上端A所用的时间t1是多少?
(2)木杆通过圆筒AB所用的时间t2是多少?(取g=10m/s2)
分析 (1)根据位移公式求解出h=$\frac{1}{2}$gt2棒下落15m和20m的时间,再求解差值得到经过圆筒的上端A所用的时间;
(2)根据位移公式求解出h=$\frac{1}{2}$gt2棒下落15m和25m的时间,再求解差值得到经过圆筒的时间,
解答 解:(1)木杆由静止开始做自由落体运动,木杆的下端到达圆筒上端A用时:
${t}_{下A}=\sqrt{\frac{2{h}_{下A}}{g}}=\sqrt{\frac{2×15}{10}}=\sqrt{3}s$
木杆的上端到达圆筒上端A用时:
${t}_{上A}=\sqrt{\frac{2{h}_{上A}}{g}}=\sqrt{\frac{2×20}{10}}=2s$
则通过圆筒上端A所用的时间:
${t}_{1}={t}_{上A}-{t}_{下A}=(2-\sqrt{3})s$
(2)木杆的下端到达圆筒上端A用时“
${t}_{下A}=\sqrt{\frac{2{h}_{下A}}{g}}=\sqrt{\frac{2×15}{10}}=\sqrt{3}s$
木杆的上端离开圆筒下端B用时:
${t}_{上B}=\sqrt{\frac{2{h}_{上B}}{g}}=\sqrt{\frac{2×25}{10}}=\sqrt{5}s$
则木杆通过圆筒所用的时间:
${t}_{2}={t}_{上B}-{t}_{下A}=(\sqrt{5}-\sqrt{3})s$
答:(1)木杆经过圆筒的上端A所用的时间t1是(2-$\sqrt{3}$)s;
(2)木杆通过圆筒AB所用的时间t2是($\sqrt{5}-\sqrt{3}$)s.
点评 本题考查自由落体运动的高度与时间的关系,只要确定了物体下落的高度,即可由h=$\frac{1}{2}$gt2求解.

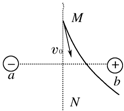 在图中,a、b带等量异种电荷,MN为ab连线的中垂线,现有一个带电粒子从M点以一定初速度v0射入,开始时一段轨迹如图中实线,不考虑粒子重力,则下列有关粒子在飞越该电场的整个过程中的说法不正确的是( )
在图中,a、b带等量异种电荷,MN为ab连线的中垂线,现有一个带电粒子从M点以一定初速度v0射入,开始时一段轨迹如图中实线,不考虑粒子重力,则下列有关粒子在飞越该电场的整个过程中的说法不正确的是( )| A. | 该粒子带负电 | |
| B. | 该粒子的动能先增大,后减小 | |
| C. | 该粒子所经位置的电势先降低,后升高 | |
| D. | 该粒子运动到无穷远处后,速度的大小一定仍为v0 |
| A. | 12 m 1.4s | B. | 12 m 2s | C. | 9.8 m 1.4s | D. | 10 m 1.4s |
| A. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此,光子散射后波长变长 | |
| B. | 考古学家发现某一骸骨中碳14的含量为活着的生物含量的四分之一,已知碳14的半衰期为5730年,则确定该生物死亡距今11460年 | |
| C. | 按照波尔理论,氢原子核外电子从较小半径跃迁到较大半径轨道时,电子的动能减少,原子总能量增大 | |
| D. | 卢瑟福发现了中子,汤姆孙发现了电子 | |
| E. | 机场、车站等地方进行安检工作时,能轻而易举地窥见箱内物品,利用了γ射线较强的穿透能力 |
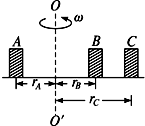 如图所示,A、B、C三个小物体放在水平旋转的圆盘上,它们与圆盘间的最大静摩擦力与其重力成正比,比例系数均为k.已知mA=2mB=2mC,rC=2rA=2rB,圆台以角速度ω旋转时,A、B、C均没有滑动,则( )
如图所示,A、B、C三个小物体放在水平旋转的圆盘上,它们与圆盘间的最大静摩擦力与其重力成正比,比例系数均为k.已知mA=2mB=2mC,rC=2rA=2rB,圆台以角速度ω旋转时,A、B、C均没有滑动,则( )| A. | C的向心加速度最大 | |
| B. | B所受静摩擦力最大 | |
| C. | 当圆盘转速逐渐增大时,C比B先开始滑动 | |
| D. | 当圆盘转速逐渐增大时,A比B先开始滑动 |

 如图所示,在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的部分轨迹,已知图中小方格的边长为L,则小球平抛的初速度v0=2$\sqrt{gL}$,b点的速度vb=$\frac{5}{2}\sqrt{gL}$.(计算结果用L、g表示)
如图所示,在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的部分轨迹,已知图中小方格的边长为L,则小球平抛的初速度v0=2$\sqrt{gL}$,b点的速度vb=$\frac{5}{2}\sqrt{gL}$.(计算结果用L、g表示)