题目内容
12. 已知氢原子处于基态能级时能量为E1,处于量子数为n的激发态能级时能量为$\frac{{E}_{1}}{{n}^{2}}$,现有一群氢原子处于n=3的激发态能级,在向低能级跃迁过程中,能放出若干种频率的光子,用它们照射某金属表面,发现从n=2能级向n=1能级跃迁时辐射出的光恰能使该金属发生光电效应,求:
已知氢原子处于基态能级时能量为E1,处于量子数为n的激发态能级时能量为$\frac{{E}_{1}}{{n}^{2}}$,现有一群氢原子处于n=3的激发态能级,在向低能级跃迁过程中,能放出若干种频率的光子,用它们照射某金属表面,发现从n=2能级向n=1能级跃迁时辐射出的光恰能使该金属发生光电效应,求:(1)该金属的极限频率;
(2)能从该金属表面逸出的光电子的最大初动能;
(3)若用光照的办法使处于n=3能级的氢原子电离,则照射光频率至少多大.
分析 (1)根据W=hγ0即可求解.
(2)根据爱因斯坦光电效应方程,结合能级差公式,求解光电子的最大初动能;
(3)根据hγ=Em-En,能级间跃迁辐射的光子能量等于两能级间的能级差,可知电离需要的最小能量,从而即可求解.
解答 解:(1)由WA=hγ0
即得:WA=$\frac{{E}_{1}}{4}$-E1=-$\frac{3}{4}$E1;
解得:γ0=$\frac{{W}_{A}}{h}$=-$\frac{3{E}_{1}}{4h}$;
(2)氢原子从n=3能级向n=1能级跃迁辐射出的光子能量最大,此时从金属表面逸出的光电子的最大初动能为Ekm
则有:hγ=$\frac{{E}_{1}}{9}$-E1=-$\frac{8}{9}$E1;
由EKm=hγ-WA解得:EKm=-$\frac{8}{9}$E1-(-$\frac{3}{4}$E1)=-$\frac{5}{36}$E1;
(3)因为放出的光子能量满足hγ=Em-En,可知,从n=3能级跃迁到无穷远需要的最小能量为:△E=0-($\frac{{E}_{1}}{{3}^{2}}$)=-$\frac{{E}_{1}}{9}$.
那么对应的频率为:f′=$-\frac{{E}_{1}}{9h}$;
答:(1)该金属的极限频率-$\frac{3{E}_{1}}{4h}$;
(2)该金属表面逸出的光电子的最大初动能-$\frac{5}{36}$E1;
(3)若用光照的办法使处于n=3能级的氢原子电离,则照射光频率至少为$-\frac{{E}_{1}}{9h}$.
点评 考查爱因斯坦光电效应方程,掌握发生光电效应现象的条件:入射光的频率大于或等于极限频率.当发生光电效应时,入射光的频率越高,而金属的逸出功是一定,则光电子的最大初动能越大.关键能级间跃迁辐射和吸收光子能量所满足的规律,即Em-En=hv,及电离的含义.

 学业测评一课一测系列答案
学业测评一课一测系列答案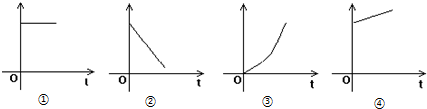
| A. | 图①是加速度--时间图象 | B. | 图②是加速度--时间图象 | ||
| C. | 图③是位移--时间图象 | D. | 图④是速度--时间图象 |
| A. | 滑块在前3s内的平均速度$\overline{v}$=7.5m/s | |
| B. | 滑块在第1s内和第2s内的位移之比为2:1 | |
| C. | 滑块在前4s内的位移为零 | |
| D. | 滑块在第3s内的平均速度$\overline{v}$=-7.5m/s |

Ⅰ.将质量为9.30×10-3kg的固体放入注射器内;
Ⅱ.缓慢推动活塞至某一位置,记录活塞所在位置的容积刻度V及对应的气体压强P;
Ⅲ.重复步骤Ⅱ,记录几组P、V值;
Ⅳ.处理记录的数据,算出固体的密度.
(1)纵坐标取V,横坐标取$\frac{1}{P}$,请根据表格数据在方格图中(图2)画出相应图线;
(2)如果图线与纵坐标的截距为b,b表示的物理意义是固体的体积,写出图线对应的函数表达式:$V=b+0.7\frac{1}{p}$;
(3)该固体的密度为$3.1×1{0}_{\;}^{3}$kg/m3.
| 测量次数 物理量 | 1 | 2 | 3 | 4 |
| P/105Pa | 0.77 | 1.00 | 1.33 | 1.82 |
| v/10-5m3 | 1.20 | 1.00 | 0.85 | 0.65 |
 如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BC在B处平滑连接,AB间的距离x=4m,B、C分别为半圆轨道的最低点和最高点,半圆轨道半径R=0.4m.一个质量m=0.1kg的小物体P在A点以一定的初速度向B点运动,后滑上半圆轨道,并恰好能经过C点.已知小物体P与水平轨道间的动摩擦因数μ=0.2,g取10m/s2.求
如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BC在B处平滑连接,AB间的距离x=4m,B、C分别为半圆轨道的最低点和最高点,半圆轨道半径R=0.4m.一个质量m=0.1kg的小物体P在A点以一定的初速度向B点运动,后滑上半圆轨道,并恰好能经过C点.已知小物体P与水平轨道间的动摩擦因数μ=0.2,g取10m/s2.求 如图是新兴的体育比赛“冰壶运动”的场地平面示意图.其中,内圆的半径为0.6m,外圆的半径为1.8m,栏线A点距内圆的圆心O点为30m,比赛时,若参赛一方将已方的冰石壶推至内圆内,并将对方冰石壶击出外圆,则获胜.在某次比赛中,甲队队员以速度v1=3m/s将质量为m=19kg的冰石壶从左侧栏线A处向右推出,恰好停在O点处.乙队队员以速度v2=5m/s将质量为M=20kg的冰石壶也从A处向右推出,沿中心线滑动到O点并和甲队冰石壶发生碰撞.设两个冰石壶均可看成质点且碰撞前后均沿中心线运动,不计碰撞时的动能损失,两个冰石壶与水平面的动摩擦因数相同.求:
如图是新兴的体育比赛“冰壶运动”的场地平面示意图.其中,内圆的半径为0.6m,外圆的半径为1.8m,栏线A点距内圆的圆心O点为30m,比赛时,若参赛一方将已方的冰石壶推至内圆内,并将对方冰石壶击出外圆,则获胜.在某次比赛中,甲队队员以速度v1=3m/s将质量为m=19kg的冰石壶从左侧栏线A处向右推出,恰好停在O点处.乙队队员以速度v2=5m/s将质量为M=20kg的冰石壶也从A处向右推出,沿中心线滑动到O点并和甲队冰石壶发生碰撞.设两个冰石壶均可看成质点且碰撞前后均沿中心线运动,不计碰撞时的动能损失,两个冰石壶与水平面的动摩擦因数相同.求: 某游乐场水上滑梯的简化模型如图所示:倾角θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7m,BC长d=2m,端点C距水面的高度h=1m.质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.1.已知cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点,g取10m/s2.求:
某游乐场水上滑梯的简化模型如图所示:倾角θ=37°斜滑道AB和水平滑道BC平滑连接,起点A距水面的高度H=7m,BC长d=2m,端点C距水面的高度h=1m.质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.1.已知cos37°=0.8,sin37°=0.6,运动员在运动过程中可视为质点,g取10m/s2.求: