题目内容
8.一个滑雪运动员从短坡顶瑞开始由静止匀加速滑下,短坡长度为9米,运动员经3秒滑至底端.求,(1)运动员下滑的加速度?
(2)运动员下滑到底端的速度是多少?
分析 根据匀变速直线运动的位移时间公式求出运动员的加速度,根据速度时间公式求出运动员滑动底端的速度
解答 解:(1)根据x=$\frac{1}{2}a{t}^{2}$得运动员的加速度为:
a=$\frac{2x}{{t}^{2}}=\frac{2×9}{{3}^{2}}m/{s}^{2}=2m/{s}^{2}$,
(2)运动员滑至底端的速度为:
v=at=2×3m/s=6m/s.
答:(1)运动员的加速度为2m/s2;
(2)运动员滑至底端的速度为6m/s.
点评 解决本题的关键掌握匀变速直线运动的位移时间公式、速度时间公式,并能灵活运用,基础题

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
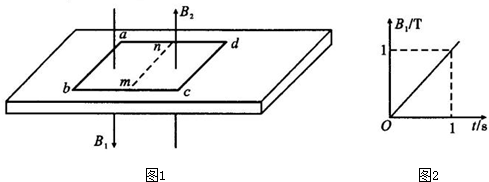
7.如图1所示,正方形线框abcd放在绝缘水平面上,导体框的质量为m=1kg,边长L=1m,电阻R=0.1Ω,mn为bc边中垂线,由t=0时刻开始在mn左侧的线框区域内加一竖直向下的磁场,其磁感应强度随时间的变化规律如图2所示,在mn右侧的线框区域内加一竖直向上、磁感应强度为B2=0.5T的匀强磁场,线框abcd的四边为磁场的边界.若导线框与长板间的最大静摩擦力等于滑动摩擦力,它们之间的动摩擦因数μ=0.3,g=10m/s2,则下列说法正确的是( )

| A. | 导线框中的感应电动势为0.5V | |
| B. | t=0.5s时刻,导线框中感应电流为0 | |
| C. | 导线框中产生俯视逆时针方向的感应电流 | |
| D. | 导线框一直静止在绝缘水平面上 |
19.(多选)在牛顿第二定律的数学表达式F=kma中,有关比例系数k的说法正确的是( )
| A. | 在任何情况下k都等于1 | |
| B. | 在国际单位制中k一定等于1 | |
| C. | k的数值由质量、加速度和力的大小决定 | |
| D. | k的数值由质量、加速度和力的单位决定 |
16. 如图所示,A、B叠放在水平面上,水平力F作用在A上,使二者一起向左做匀速直线运动,下列说法正确的是( )
如图所示,A、B叠放在水平面上,水平力F作用在A上,使二者一起向左做匀速直线运动,下列说法正确的是( )
 如图所示,A、B叠放在水平面上,水平力F作用在A上,使二者一起向左做匀速直线运动,下列说法正确的是( )
如图所示,A、B叠放在水平面上,水平力F作用在A上,使二者一起向左做匀速直线运动,下列说法正确的是( )| A. | A、B之间无摩擦力 | B. | A受到的静摩擦力水平向右 | ||
| C. | B受到A的静摩擦力水平向左 | D. | 地面对B的滑动摩擦力水平向右 |
3.下列说法正确的是( )
| A. | 由R=$\frac{U}{I}$知,导体的电阻与导体两端电压成正比,与流过导体的电流成反比 | |
| B. | 由I=$\frac{U}{R}$知,导体中的电流与导体两端电压成正比,跟导体的电阻成反比 | |
| C. | 由ρ=$\frac{RS}{I}$知,导体的电阻率与导体的电阻和横截面积的乘积成正比,与导体的长度成反比 | |
| D. | 公式W=UIt适用于任何电路;Q=I2Rt求热时仅适用于纯电阻电路 |
13.关于瞬时速度,下列说法正确的是( )
| A. | 是物体在某段时间内的速度 | |
| B. | 是物体在某一时刻的速度 | |
| C. | 是物体在发生某一段位移过程中的速度 | |
| D. | 是物体通过某一位置时的速度 |
20.如图所示,质量为m的物块始终静止在倾角为θ的斜面上,下列说法中正确的是( )


| A. | 若斜面水平向右匀速移动距离S,斜面对物块一定做功 | |
| B. | 若斜面竖直向上匀速移动距离S,斜面对物块做功mgS | |
| C. | 若斜面水平向左以加速度a移动距离S,斜面对物块做功maS | |
| D. | 若斜面竖直向下以加速度a移动距离S,斜面对物块做功m(g+a)S |
18.唐僧、悟空、沙僧和八戒师徒四人想划船渡过一条河,他们观察到河水的流速为5m/s,已知他们在静水中划船的速度为4m/s,对于这次划船过河,他们各自看法正确的是( )
| A. | 唐僧说:我们要想到达正对岸就得朝着正对岸划船 | |
| B. | 悟空说:我们要想节省时间就得船头偏向上游朝着对岸划船 | |
| C. | 沙僧说:我们要想少走点路就得朝着正对岸划船 | |
| D. | 八戒说:今天这种情况我们是不可能到达正对岸的 |
 如图所示,质量为M的支架静止于水平地面上,质量为m的小球(可视为质点)用长度为L的轻绳系着,绕竖直放置支架上的悬点在竖直平面内做圆周运动,已知悬点距水平地面的竖直距离为H,已知重力加速度g.
如图所示,质量为M的支架静止于水平地面上,质量为m的小球(可视为质点)用长度为L的轻绳系着,绕竖直放置支架上的悬点在竖直平面内做圆周运动,已知悬点距水平地面的竖直距离为H,已知重力加速度g.