题目内容
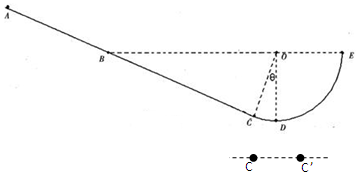
13. 如图所示,AB是固定的光滑半球体的水平直径,O为半球体的球心,C是半球体的最高点;将一小球从C处由静止释放,受到微小扰动后小球沿半球滑下,滑到P点时脱离半球,OP与OB夹角为θ,则sinθ=( )
如图所示,AB是固定的光滑半球体的水平直径,O为半球体的球心,C是半球体的最高点;将一小球从C处由静止释放,受到微小扰动后小球沿半球滑下,滑到P点时脱离半球,OP与OB夹角为θ,则sinθ=( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 从C到P根据动能定理求得到达P点的速度,在P点恰好脱离轨道,对轨道无压力,根据牛顿第二定律1求得
解答 解:设到达P点时,脱离半球,从C到P根据动能定理可知$mgR(1-sinθ)=\frac{1}{2}m{v}^{2}$
在P点,根据点根据牛顿第二定律可知$mgsinθ=\frac{m{v}^{2}}{R}$
联立解得$sinθ=\frac{2}{3}$,故C正确
故选:C
点评 本题关键是明确小球的受力情况和运动情况,关键是找到向心力来源,结合动能定理和牛顿第二定律列式求解,不难.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
14.11月17日至19日,曲靖一中体育艺术节顺利举行,本次艺术节期间,各路学霸化身体育健儿,在运动场上挥洒汗水,为班争光,并奋力冲击校记录、市记录;2017届高三年级的刘同学在急行跳远中取得了优异成绩,刘同学主炮-起跳-着地的过程中(如图所示为杨同学抓拍到的三个动作),忽略空气阻力的作用,则下列说法正确的是( )


| A. | 刘同学在助跑动作①中前脚向后蹬地,此时他所受的摩擦力向后 | |
| B. | 刘同学在起跳过程中有动作②(双脚未离地),则他在起跳中地面给他的支持力做正功,让他获得了一个初速度 | |
| C. | 刘同学在空中运动时,动量守恒,机械能守恒 | |
| D. | 刘同学在着地过程中有一缓冲动作③(双脚接地),则在缓冲过程中地面给他的支持力的冲量不等于他动量的减小量 |
1. 如图所示,竖直固定的半径为R的光滑圆形制内,一可视为质点的小球通过轨道最低点P时,加速度大小为2g.已知重力加速度为g,不计空气阻力,下列说法正确的是( )
如图所示,竖直固定的半径为R的光滑圆形制内,一可视为质点的小球通过轨道最低点P时,加速度大小为2g.已知重力加速度为g,不计空气阻力,下列说法正确的是( )
 如图所示,竖直固定的半径为R的光滑圆形制内,一可视为质点的小球通过轨道最低点P时,加速度大小为2g.已知重力加速度为g,不计空气阻力,下列说法正确的是( )
如图所示,竖直固定的半径为R的光滑圆形制内,一可视为质点的小球通过轨道最低点P时,加速度大小为2g.已知重力加速度为g,不计空气阻力,下列说法正确的是( )| A. | 小球过P点时速度大小为$\sqrt{2gR}$ | B. | 小球能沿轨道做完整圆周运动 | ||
| C. | 小球运动的最小加速度为0 | D. | 小球运动的最小速度为0 |
5.传统的自行车发电机内部电路如图甲所示,驱动轴一端与自行车车轮相连,另一端连接条形永磁铁,车轮转动过程中,驱动轴带动磁铁在铁芯之间匀速转动,发电机线圈两端产生的交变电压波形如图乙所示.已知波形图中正负尖峰电压分别为Um和-Um.两个相邻正、负尖峰电压所对应的时间差为△t,发电机线圈匝数为n.以下判断正确的是( )


| A. | 该交流电的周期为△t | |
| B. | 驱动轴转动的角速度ω=$\frac{2π}{△t}$ | |
| C. | 线圈电压的有效值U=$\frac{\sqrt{2}{U}_{m}}{2}$ | |
| D. | 穿过线圈磁通量变化率的最大值$(\frac{△φ}{△t})_{max}$=$\frac{{U}_{m}}{n}$ |
2.若某星球的密度是地球密度的2倍,它表面的重力加速度与地球相同,则该星球的质量是地球质量的( )
| A. | $\frac{1}{4}$ | B. | 4倍 | C. | 8倍 | D. | 16倍 |
3.一同学用多用电表测量某未知电阻,其测量方法完全正确,已知其选择开关在“×10”档,指针停在表盘中央附近,其表盘读数是30,那么该未知电阻的阻值是( )
| A. | 3Ω | B. | 30Ω | C. | 40Ω | D. | 300Ω |
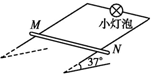 如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为1m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.一导体棒MN垂直于导轨放置,质量为0.5kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为1T.将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,求此后导体棒MN的运动速度以及小灯泡消耗的电功率(重力加速度g取10m/s2,sin 37°=0.6)
如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为1m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.一导体棒MN垂直于导轨放置,质量为0.5kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为1T.将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,求此后导体棒MN的运动速度以及小灯泡消耗的电功率(重力加速度g取10m/s2,sin 37°=0.6)