��Ŀ����
19����ÿ���ʱ�2014��4��18�ձ������������Һ��պ���֣�NASA��Ŀǰ�����״���̫��ϵ�ⷢ�֡���ء�����Kepler-186f�������Ա��������ɴ���������ǣ����п�ѧ�۲⣺��������ת����ΪT���Ա�ڸ����ǡ�������������ǵ��渽��h�������ͷ�һ��С��������Ϊ�����������ʱ��Ϊt����֪�����ǰ뾶ΪR��������������ΪG��������˵����ȷ���ǣ�������| A�� | �����ǵ�ƽ���ܶ�Ϊ$\frac{3h}{{2��GR{t^2}}}$ | |
| B�� | �����ǵĵ�һ�����ٶ�Ϊ$\frac{��R}{T}$ | |
| C�� | ����ɴ��Ƹ�������Բ���˶������ڲ�С�ڦ�t$\sqrt{\frac{2R}{h}}$ | |
| D�� | ��������Ǵ���һ��ͬ�����ǣ�������DZ���߶�Ϊ$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{��}^{2}{t}^{2}}}$ |
���� �������������˶�������������������ٶȣ��ٸ������������ṩԲ���˶�������������������˶������ڣ�������$��=\frac{M}{V}$���Ӷ�������⣮
��� �⣺�������������˶�������������������ٶ�g=$\frac{2h}{{t}^{2}}$
A����G$\frac{Mm}{{R}^{2}}$=mg=m$\frac{2h}{{t}^{2}}$�У�M=$\frac{2h{R}^{2}}{G{t}^{2}}$������������ܶȦ�=$\frac{M}{V}$=$\frac{3h}{2G{t}^{2}R��}$����A��ȷ��
B������ĵ�һ�����ٶ�v=$\sqrt{gR}$=$\sqrt{\frac{2h}{{t}^{2}}R}$����B����
C���������������ṩԲ���˶��������У�G$\frac{Mm}{{r}^{2}}$=mr$\frac{4{��}^{2}}{{T}^{2}}$
�ɵ����ǵ�����T=$\sqrt{\frac{4{��}^{2}{r}^{3}}{GM}}$����֪����뾶ԽС����ԽС�����ǵ���С�뾶ΪR����������СֵΪTmin=$\sqrt{\frac{4{��}^{2}{R}^{3}}{GM}}$=$\sqrt{\frac{4{��}^{2}R}{\frac{2h}{{t}^{2}}}}$=��t$\sqrt{\frac{2R}{h}}$����C��ȷ��
D��ͬ�����ǵ�������������ת������ͬ���У�G$\frac{Mm}{��R+h��^{2}}$=m��R+h��$\frac{4{��}^{2}}{{T}^{2}}$���������ݽ�ã�h=$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{��}^{2}{t}^{2}}}$-R����D����
��ѡ��AC��
���� ����ؼ���ͨ�����������˶�������������������ٶȣ��ٸ������������ṩԲ���˶���������������������������⣮

| A�� | ���������������ԭ�ӵĺ�ʽ�ṹѧ˵ | |
| B�� | ��ķ��ͨ�����������ߵ��о������˵��ӣ��Ӷ�֤����ԭ�Ӻ˿��ٷ� | |
| C�� | ���ʿ���1900�����������������ѧ����ȷ���Ƴ��ˡ����������仯���Ĵ�ͳ���� | |
| D�� | ����˹̹Ϊ�����ЧӦ��ʵ���������˹���˵ |
 ͼʾΪת�ִ���װ�ã�����������û�д�����A��B��C�����λ�ù�ϵ��ͼ����O1C=r2������������ļ��ٶȵĹ�ϵΪ��������
ͼʾΪת�ִ���װ�ã�����������û�д�����A��B��C�����λ�ù�ϵ��ͼ����O1C=r2������������ļ��ٶȵĹ�ϵΪ��������| A�� | aA=aB=aC | B�� | aC��aA��aB | C�� | aC��aA��aB | D�� | aC=aB��aA |
 ijѧ���������о�ƽ���˶�����ʵ���У����Ǽ���С����ƽ���˶������λ�ã�OΪ�����˶�һ��ʱ����λ�ã�ȡΪ����ԭ�㣬ƽ�Ĺ켣��ͼʾ�����ݹ켣���������������ƽ���˶��ij��ٶ�Ϊv0=1m/s���׳��������Ϊ��-10cm��-5cm��
ijѧ���������о�ƽ���˶�����ʵ���У����Ǽ���С����ƽ���˶������λ�ã�OΪ�����˶�һ��ʱ����λ�ã�ȡΪ����ԭ�㣬ƽ�Ĺ켣��ͼʾ�����ݹ켣���������������ƽ���˶��ij��ٶ�Ϊv0=1m/s���׳��������Ϊ��-10cm��-5cm��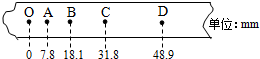 ����֤��е���غ㶨�ɡ���ʵ�����������������ķ�����
����֤��е���غ㶨�ɡ���ʵ�����������������ķ����� ��ͼ����ǿ�糡�ij�ǿΪ103V/m��a��b�����ľ���Ϊ0.1m��ab������糡����ļн�Ϊ60�㣬��a��b�����ĵ��Ʋ�Ϊ50V����������Ϊ-2��10-10C�ĵ��ɴ�a���Ƶ�b�㣬�糡������Ϊ1��10-8 J��
��ͼ����ǿ�糡�ij�ǿΪ103V/m��a��b�����ľ���Ϊ0.1m��ab������糡����ļн�Ϊ60�㣬��a��b�����ĵ��Ʋ�Ϊ50V����������Ϊ-2��10-10C�ĵ��ɴ�a���Ƶ�b�㣬�糡������Ϊ1��10-8 J��