题目内容
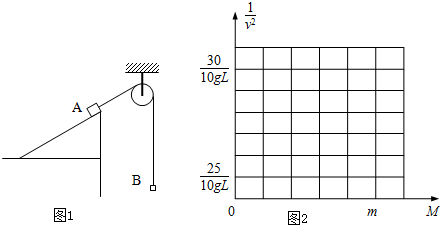
利用如图装置研究均匀规则重滑轮的转动动能。长L、倾角30°的光滑斜面固定在桌角。质量为2m的小物体A与质量为mB的小物体B用长轻绳绕过半径R的定滑轮连接,A与滑轮之间的绳子与斜面平行。将A从斜面顶端静止释放,测得到达斜面底端时的速度v,逐渐减小定滑轮质量M,多次测量得![]() 关系表。已知L、g、m、R,不计滑轮转轴处摩擦,绳与滑轮不打滑。求:
关系表。已知L、g、m、R,不计滑轮转轴处摩擦,绳与滑轮不打滑。求:
(1)作出![]() 图。
图。
(2)对图像做合理推广,求mB
(3)质量m的滑轮以角速度ω转动时,用m、R、ω表示出动能。
(4)取下B,将绳子缠绕在质量m的滑轮边缘,使A释放后匀加速下滑时能不打滑带动它,求A的加速度。
| ||||||||||||||
 | ||||||||||||||

(1)图略,为一直线…………2分
(2)图像截距![]() ,含义是滑轮不计质量时,速度平方的倒数。
,含义是滑轮不计质量时,速度平方的倒数。
对AB的运动过程分析,根据动能定理(或机械能守恒)有
![]() …………2分
…………2分
代入v2= ![]() ,
,
得mB=0.5m…………2分
(3)取质量为m的滑轮数据分析,设A滑动到底部时滑轮动能EK
对AB的运动过程分析,根据动能定理(或机械能守恒)有
![]() …………2分
…………2分
EK= mgL/2—5mv2/4
代入v2= ![]() ,
,
得EK= mv2/4= ![]() …………2分
…………2分
注:若有学生直接用刚体转动动能公式Jω2/2求解,其中转动惯量J=mR2/2,则必须给出J的积分计算过程。
(4)根据(3)问结果,对整体列A下滑过程的动能定理(或机械能守恒)有
![]() …………2分
…………2分
得v2= ![]()
加速度a= v2/2L= ![]() …………2分
…………2分
注:若有学生直接用刚体的转动定律,则有mg-T=2ma,TR=Jβ,其中转动惯量J=mR2/2,若第3问已给出J的积分计算过程,则此问不需再次给出。β为角加速度,满足β=a/R。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
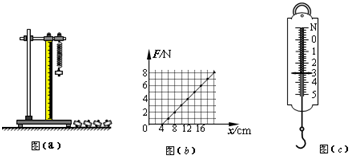 I.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验.
I.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验.