题目内容
 用长L=0.4m的轻细线一端固定在悬点O上,另一端拴一个质量为2kg小球,现用力将小球拉至与O点在同一水平面上的A点后无初速度释放,此后小球沿
用长L=0.4m的轻细线一端固定在悬点O上,另一端拴一个质量为2kg小球,现用力将小球拉至与O点在同一水平面上的A点后无初速度释放,此后小球沿| 1 | 4 |
(1)小球刚到达B点时的速度大小;
(2)小球运动到B点时,绳断前瞬间对小球的拉力;
(3)小球进入弧面轨道后,运动过程中始终未脱离轨道,不计在过渡圆弧处的机械能损失,小球在弧面CD上最远滑行到D点,求小球在弧面轨道BCD上由B点运动到D点过程中克服摩擦力做的功.
分析:(1)小球从A点沿圆弧运动到B点过程中,只有重力做功,根据动能定理或机械能守恒求解小球刚到达B点时的速度大小;
(2)在B点,由细线的拉力和重力的合力提供向心力,由牛顿第二定律和圆周运动知识求解.
(3)小球从B点沿轨道运动到D点过程中,运用动能定理求解克服摩擦力做的功.
(2)在B点,由细线的拉力和重力的合力提供向心力,由牛顿第二定律和圆周运动知识求解.
(3)小球从B点沿轨道运动到D点过程中,运用动能定理求解克服摩擦力做的功.
解答:解:(1)小球从A点沿圆弧运动到B点过程中,由动能定理得:
mgL=
m
解得:vB=
=2
m/s
(2)在B点,由细线的拉力和重力的合力提供向心力,则由牛顿第二定律和圆周运动知识得
T-mg=m
解得:T=m(g+
)=2×(10+
)=60N
(3)设小球从B点沿轨道运动到D点过程中克服摩擦力做的功为Wf,由动能定理得:
-Wf=0-
m
解得:Wf=
m
=
×2×(2
)2=8J
答:(1)小球刚到达B点时的速度大小是2
m/s;
(2)小球运动到B点时,绳断前瞬间对小球的拉力是60N;
(3)小球在弧面轨道BCD上由B点运动到D点过程中克服摩擦力做的功是8J.
mgL=
| 1 |
| 2 |
| v | 2 B |
解得:vB=
| 2gL |
| 2 |
(2)在B点,由细线的拉力和重力的合力提供向心力,则由牛顿第二定律和圆周运动知识得
T-mg=m
| ||
| L |
解得:T=m(g+
| ||
| L |
(2
| ||
| 0.4 |
(3)设小球从B点沿轨道运动到D点过程中克服摩擦力做的功为Wf,由动能定理得:
-Wf=0-
| 1 |
| 2 |
| v | 2 B |
解得:Wf=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| 2 |
答:(1)小球刚到达B点时的速度大小是2
| 2 |
(2)小球运动到B点时,绳断前瞬间对小球的拉力是60N;
(3)小球在弧面轨道BCD上由B点运动到D点过程中克服摩擦力做的功是8J.
点评:本题是动能定理与圆周运动动力学的综合,是常见的题型,它们之间的纽带是速度,要能熟练运用动能定理求解变力的功.

练习册系列答案
相关题目



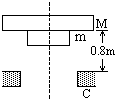 如图所示,两块大小不同、质量分别为M和m的圆形薄板(厚度不计),半径分别为R和r,M=3m,两板之间用一根长为L=0.4m的轻绳相连结,开始时两板水平放置并叠合在一起处在静止状态,在其正下方0.8m处有一固定支架C,支架上有一半径为R'(r<R'<R)的圆孔,圆孔与两薄板中心均在圆孔中心轴线上,今使两板一起无初速自由下落,空气阻力忽略不计.大板与支架C发生没有机械能损失的弹性碰撞,碰撞后,两块板即分离,直到轻绳绷紧,在轻绳绷紧的瞬间,两板便获得共同速度.试求这个共同速度的大小.(g取m/
如图所示,两块大小不同、质量分别为M和m的圆形薄板(厚度不计),半径分别为R和r,M=3m,两板之间用一根长为L=0.4m的轻绳相连结,开始时两板水平放置并叠合在一起处在静止状态,在其正下方0.8m处有一固定支架C,支架上有一半径为R'(r<R'<R)的圆孔,圆孔与两薄板中心均在圆孔中心轴线上,今使两板一起无初速自由下落,空气阻力忽略不计.大板与支架C发生没有机械能损失的弹性碰撞,碰撞后,两块板即分离,直到轻绳绷紧,在轻绳绷紧的瞬间,两板便获得共同速度.试求这个共同速度的大小.(g取m/