题目内容
6.一质量为0.5kg的小球A以2.0m/s的速度和静止于光滑水平面上质量为1kg的另一大小相同的小球B发生正碰,碰撞后A以0.2m/s的速度反弹.求:(1)碰撞过程小球A动量的变化△P
(2)碰撞后小球B获得的速度大小;
(3)通过计算说明此碰撞是弹性碰撞还是非弹性碰撞.
分析 (1)根据动量定理即可求出动量的变化;
(2)碰撞过程中动量守恒,由动量守恒定律可以求出小球速度.
(3)由能量守恒定律可以求出损失的机械能,然后进行判定.
解答 解:(1)根据动量定理得小球A动量的变化:△P=P2-P1;△P=1.1kg•m/s
方向与初速度方向相反
(2)选取A的初速度的方向为正方向,A与B碰撞的过程中动量守恒,根据动量守恒定律得:m1v1+0=m1v+m2v2′
代入数据得:v2′=1.1 m/s
(3)碰撞的过程中损失的机械能:△E=$\frac{1}{2}$m1v${\;}_{1}^{2}$-$\frac{1}{2}$m1v1′2-$\frac{1}{2}$m2v2′2=0.385 J>0,所以该碰撞是非弹性碰撞
答:(1)碰撞过程小球A动量的变化是1.1kg•m/s,方向与初速度方向相反;(2)碰撞后小球B获得的速度大小是1.1m/s;(3)此碰撞是非弹性碰撞.
点评 小球碰撞过程中动量守恒、机械能不守恒,由动量守恒定律与能量守恒定律可以正确解题,应用动量守恒定律解题时要注意正方向的选择.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.宇航员乘飞船前往A星球,其中有一项任务是测该星球的密度.已知该星球的半径为R,引力常量为G.结合已知量有同学为宇航员设计了以下几种测量方案.你认为正确的是( )
| A. | 当飞船绕星球在任意高度运行时测出飞船的运行周期T | |
| B. | 当飞船绕星球在任意高度运行时测出飞船的运行周期T和飞船到星球的距离h | |
| C. | 当飞船绕星球表面运行时测出飞船的运行周期T | |
| D. | 当飞船着陆后宇航员测出该星球表面的重力加速度g |
18.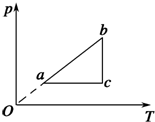 一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其pT图象如图所示.下列判断正确的是( )
一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其pT图象如图所示.下列判断正确的是( )
 一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其pT图象如图所示.下列判断正确的是( )
一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其pT图象如图所示.下列判断正确的是( )| A. | 过程ab中气体一定吸热 | |
| B. | a和c两个状态中,容器壁单位面积、单位时间内受到气体分子撞击的次数不同 | |
| C. | 过程ca中外界对气体所做的功等于气体所放的热 | |
| D. | a、b和c三个状态中,状态a分子的平均动能最小 |
16.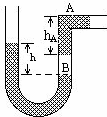 如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
 如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )| A. | 图中h减小 | B. | 空气柱B的长度不变 | ||
| C. | 空气柱B的压强增大 | D. | 图中h不变 |
 在“测定金属的电阻率”的实验中,用螺旋测微器测量金属直径D的刻度位置如图所示,用米尺测出金属丝的长L,金属丝的电阻大约为5Ω.先用伏安法测出金属丝的电阻R,然后根据电阻定律计算出该金属材料的电阻率ρ.为此取来两节新的干电池、电键和若干导线及下列器材:
在“测定金属的电阻率”的实验中,用螺旋测微器测量金属直径D的刻度位置如图所示,用米尺测出金属丝的长L,金属丝的电阻大约为5Ω.先用伏安法测出金属丝的电阻R,然后根据电阻定律计算出该金属材料的电阻率ρ.为此取来两节新的干电池、电键和若干导线及下列器材: 质量为m的飞机以恒定速率v在空中水平盘旋,做匀速圆周运动的半径为R,重力加速度为g,则此时飞机做圆周运动的向心力为$m\frac{{v}^{2}}{R}$,空气对飞机的作用力大小为$m\sqrt{{g}^{2}+\frac{{v}^{4}}{{R}^{2}}}$.
质量为m的飞机以恒定速率v在空中水平盘旋,做匀速圆周运动的半径为R,重力加速度为g,则此时飞机做圆周运动的向心力为$m\frac{{v}^{2}}{R}$,空气对飞机的作用力大小为$m\sqrt{{g}^{2}+\frac{{v}^{4}}{{R}^{2}}}$.



 如图所示,在长为L的细绳一端系一个质量为m的小球A,小球绕绳的另一固定端O点在竖直平面内做圆周运动,已知小球恰好能经过最高点,且经过最低点的拉力大小为6mg,不计空气阻力,重力加速度为g,求:
如图所示,在长为L的细绳一端系一个质量为m的小球A,小球绕绳的另一固定端O点在竖直平面内做圆周运动,已知小球恰好能经过最高点,且经过最低点的拉力大小为6mg,不计空气阻力,重力加速度为g,求: 如图所示,圆管构成的半圆形轨道竖直固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止在该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为4R,重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求:
如图所示,圆管构成的半圆形轨道竖直固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止在该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为4R,重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求: