题目内容
5. 如图所示,在空间中存在着方向为水平方向的匀强磁场,磁感强度为B.一个带电荷量为q、质量为m的微粒从图中的a处由静止释放,它运动的轨迹如图中的曲线所示,其中b点为轨迹的最低点,c与a点在同一水平面内,此后将重复这一阶段的运动.下面关于最低点b的说法中不正确的是( )
如图所示,在空间中存在着方向为水平方向的匀强磁场,磁感强度为B.一个带电荷量为q、质量为m的微粒从图中的a处由静止释放,它运动的轨迹如图中的曲线所示,其中b点为轨迹的最低点,c与a点在同一水平面内,此后将重复这一阶段的运动.下面关于最低点b的说法中不正确的是( )| A. | 微粒经过b点时的速度方向为水平方向 | |
| B. | 微粒经过b点时受到的磁场力与重力大小相等而方向相反 | |
| C. | 微粒经过b点时的速度大于$\frac{mg}{Bq}$ | |
| D. | 微粒经过b点时的重力势能与动能之和等于在a点时的重力势能 |
分析 该题中,微粒从a点出发,先向下运动,然后在洛伦兹力的作用下,运动的轨迹发生偏转,由题可知,若将微粒的运动看做是在重力和磁场力的作用下,是向右匀速直线运动与逆时针方向的匀速圆周运动的合运动,则微粒的运动具有周期性与对称性,微粒的受力也具有周期性与对称性,微粒在最高点与最低点受到的合力的方向相反,大小相等.分析微粒受到的合外力提供向心力,即可求出微粒在最低点的速度,然后由机械能守恒即可求出微粒下落的高度,由微粒在磁场中做圆周运动的特点,即可求出周期.
解答 解:A、b点为微粒轨迹的最低点,没有竖直方向的分速度,所以微粒经过b点时的速度方向为水平方向.故A正确;
B、C、由题意,可以将小球的运动可以看做是在重力和磁场力的作用下,是向右匀速直线运动与逆时针方向的匀速圆周运动的合运动,则小球的运动具有周期性与对称性,小球在最高点与最低点受到的合力的方向相反,大小相等.
小球在最高点的速度为0,只受到的重力的作用,方向向下,可知小球在最低点时,小球受到的洛伦兹力与重力的合力方向向上,大小也等于重力,即:qvB-mg=mg,所以:qvB=2mg;$v=\frac{2mg}{qB}$.故B错误,C正确;
D、由于洛伦兹力的方向始终与运动的方向垂直,洛伦兹力不做功,微粒的动能与重力势能之间相互转化,微粒经过b点时的重力势能与动能之和等于在a点时的重力势能.故D正确.
本题选择不正确的,故选:B
点评 该题考查带电微粒在重力和洛伦兹力的作用下的运动,由于洛伦兹力的大小随速度发生变化,洛伦兹力的方向也随速度的方向发生变化,所以通常的方法是使用偏微分方程来解答.该题中,由于题目给出了“小球在重力和磁场力的作用下的运动可看作是向右匀速直线运动与逆时针方向的匀速圆周运动的合运动”的特殊的方法,因此,可以结合运动的周期性和对称性,以及受力的周期性与对称性进行解答.

 如图所示,在粗糙的水平面上有两块弹性钢板M,N,两者相距为6m.一个可视为质点的小铁块以8m/s的初速度从M板向N板处运动.小铁块与M、N板相碰时不损失机械能,小铁块最终停在距离M板4m处.若小铁块和N板仅碰撞一次,则下列说法错误的是( )
如图所示,在粗糙的水平面上有两块弹性钢板M,N,两者相距为6m.一个可视为质点的小铁块以8m/s的初速度从M板向N板处运动.小铁块与M、N板相碰时不损失机械能,小铁块最终停在距离M板4m处.若小铁块和N板仅碰撞一次,则下列说法错误的是( )| A. | 小铁块通过的路程可能为16m | B. | 小铁块运动的时间可能为3s | ||
| C. | 小铁块的加速度大小可能为4m/s2 | D. | 小铁块的平均速度可能为2m/s |
 如图所示,光滑水平地面上静止放置由弹簧相连的木块A和B,开始时弹簧处于原长,现给A一个向右的瞬时冲量,让A开始以速度v0向右运动,若mA>mB,则( )
如图所示,光滑水平地面上静止放置由弹簧相连的木块A和B,开始时弹簧处于原长,现给A一个向右的瞬时冲量,让A开始以速度v0向右运动,若mA>mB,则( )| A. | 当弹簧压缩最短时,B的速度达到最大值 | |
| B. | 当弹簧再次恢复原长时,A的速度一定向右 | |
| C. | 当弹簧再次恢复原长时,A的速度一定小于B的速度 | |
| D. | 当弹簧再次恢复原长时,A的速度可能大于B的速度 |
| A. | 汽车转弯时要限制速度 | |
| B. | 转速很大的砂轮半径做得不能太大 | |
| C. | 炼钢厂把熔化钢水浇入模子,让模子高速旋转来制造无缝钢管 | |
| D. | 工作的洗衣机脱水桶转速很大 |
 如图所示,足够长的光滑导轨倾斜放置,其下端连接一个定值电阻R,匀强磁场垂直于导轨所在平面,将ab棒在导轨上无初速度释放,当ab棒下滑到稳定状态时,速度为v,电阻R上消耗的功率为P.导轨和导体棒电阻不计.下列判断正确的是( )
如图所示,足够长的光滑导轨倾斜放置,其下端连接一个定值电阻R,匀强磁场垂直于导轨所在平面,将ab棒在导轨上无初速度释放,当ab棒下滑到稳定状态时,速度为v,电阻R上消耗的功率为P.导轨和导体棒电阻不计.下列判断正确的是( )| A. | 导体棒的a端比b端电势低 | |
| B. | ab棒在达到稳定状态前做加速度减小的加速运动 | |
| C. | 若磁感应强度增大为原来的2倍,其他条件不变,则ab棒下滑到稳定状态时速度将变为原来的$\frac{1}{2}$ | |
| D. | 若换成一根质量为原来2倍的导体棒,其他条件不变,则当ab棒下滑到稳定状态时电阻R上消耗的功率将变为原来的4倍 |
 如图所示,在匀强磁场中,一矩形金属线圈两次分别以不同的转速,绕与磁感线垂直的轴匀速转动,产生的交变电动势图象如图2中曲线a、b所示,则( )
如图所示,在匀强磁场中,一矩形金属线圈两次分别以不同的转速,绕与磁感线垂直的轴匀速转动,产生的交变电动势图象如图2中曲线a、b所示,则( )| A. | 两次t=0时刻线圈平面与中性面重合 | |
| B. | 曲线a、b对应的线圈转速之比为2:3 | |
| C. | 曲线a表示的交变电动势频率为25Hz | |
| D. | 曲线b表示的交变电动势有效值为10V |
 图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )| A. | a点与b点的线速度大小相等 | B. | a点与b点的角速度大小相等 | ||
| C. | a点与d点的线速度大小相等 | D. | a点与d点的向心加速度大小相等 |
 如图所示,某人用大小不变的力F拉着放在光滑平面上的物体,开始时和物体相连的绳与水平面间的夹角是α,当拉力F作用一段时间后,绳与水平面间的夹角为β,已知图中的高度为h,求绳的拉力F对物体所做的功.(绳的质量、滑轮的质量以及绳与滑轮间的摩擦不计.)
如图所示,某人用大小不变的力F拉着放在光滑平面上的物体,开始时和物体相连的绳与水平面间的夹角是α,当拉力F作用一段时间后,绳与水平面间的夹角为β,已知图中的高度为h,求绳的拉力F对物体所做的功.(绳的质量、滑轮的质量以及绳与滑轮间的摩擦不计.)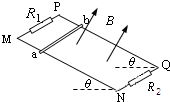 如图,MN、PQ两条平行的粗糙金属轨道与水平面成θ=37°角,轨距为L=1m,质量为m=0.6kg的金属杆ab水平放置在轨道上,其阻值r=0.1Ω.空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B=0.5T.P、M间接有R1=4Ω的电阻,Q、N间接有R2=6Ω的电阻.杆与轨道间的动摩擦因数为μ=0.5,若轨道足够长且电阻不计,现从静止释放ab,当金属杆ab运动的速度为10m/s时,求:(重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8)
如图,MN、PQ两条平行的粗糙金属轨道与水平面成θ=37°角,轨距为L=1m,质量为m=0.6kg的金属杆ab水平放置在轨道上,其阻值r=0.1Ω.空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B=0.5T.P、M间接有R1=4Ω的电阻,Q、N间接有R2=6Ω的电阻.杆与轨道间的动摩擦因数为μ=0.5,若轨道足够长且电阻不计,现从静止释放ab,当金属杆ab运动的速度为10m/s时,求:(重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8)