��Ŀ����
6�� ij��ȤС���õ�������������ij�ų��ĴŸ�Ӧǿ�ȣ�ʵ��װ����ͼ�ף����Ƶ�����㹻���⻬����������ֱ��������ǿ�ų��У�������Ϊd����ƽ����ų�����ֱ����������������ֵΪR�ĵ��贮�����ڵ����϶ˣ�����Ϊm����Ч��ֵΪr�ĵ����AB�ɾ�ֹ�ͷ��ص����»����ù����е�����������õ�����ʱ��仯������ͼ����ʾ���������ֵΪIm�����»��������뵼�챣�ִ�ֱ�����ýӴ������Ƶ������������輰�����������������ٶ�Ϊg��
ij��ȤС���õ�������������ij�ų��ĴŸ�Ӧǿ�ȣ�ʵ��װ����ͼ�ף����Ƶ�����㹻���⻬����������ֱ��������ǿ�ų��У�������Ϊd����ƽ����ų�����ֱ����������������ֵΪR�ĵ��贮�����ڵ����϶ˣ�����Ϊm����Ч��ֵΪr�ĵ����AB�ɾ�ֹ�ͷ��ص����»����ù����е�����������õ�����ʱ��仯������ͼ����ʾ���������ֵΪIm�����»��������뵼�챣�ִ�ֱ�����ýӴ������Ƶ������������輰�����������������ٶ�Ϊg����1����ôų��Ÿ�Ӧǿ�ȴ�С��
��2������t1ʱ�̰�AB���ٶȴ�С��
��3����0��t1ʱ���ڰ�AB�½��ĸ߶�Ϊh����˹��̵���R�����ĵ��ȣ�
���� ��1�����õ����ﵽ���ֵʱ�������������ֱ���˶�������ƽ������������ų��Ÿ�Ӧǿ�ȴ�С��
��2����ͼ�п�֪t1ʱ�̰��е������ֵΪIm���������ʱ��Ӧ�綯�ƣ�������ŷķ������ʽ�������̣���������t1ʱ�̰�AB���ٶȴ�С��
��3�����������غ㶨�������AB�½��ĸ߶�Ϊhʱ������·�����ĵ��ȣ�����˹��̵���R�����ĵ��ȣ�
��� �⣺��1��������Imʱ������������˶�
���������ܵ��İ�������F��=BImd
������ֱ���˶�����ƽ��������F��=mg
��ã�B=$\frac{mg}{{I}_{m}d}$��
��2��t1ʱ�̣��Ի�·�У�
��Ӧ�綯��E=Bdv
��Ӧ����${I_m}=\frac{Bdv}{R+r}$
��ã�$v=\frac{{I_m^2��{R+r}��}}{mg}$��
��3���������غ㶨�ɵõ�·�в������ܵ��ȣ�$Q=mgh-\frac{1}{2}m{v^2}$
�����R�ϲ����ĵ��ȣ�${Q_R}=\frac{R}{R+r}Q$
��ã�${Q_R}=\frac{mghR}{R+r}-\frac{{I_m^4R��{R+r}��}}{{2m{g^2}}}$
�𣺣�1���ôų��Ÿ�Ӧǿ�ȴ�СΪ$\frac{mg}{{I}_{m}d}$��
��2����t1ʱ�̰�AB���ٶȴ�СΪ$\frac{{I}_{m}^{2}��R+r��}{mg}$��
��3����0��t1ʱ���ڰ�AB�½��ĸ߶�Ϊh���˹��̵���R�����ĵ���Ϊ$\frac{mghR}{R+r}-\frac{{I}_{m}^{4}R��R+r��}{2m{g}^{2}}$��
���� ���⿼���Ÿ�Ӧ���������������غ㶨�ɣ������Ĺؼ���Ҫ��Ϥ�����и�Ÿ���ʱ��Ӧ�綯��E=BLv��Ӧ����$I=\frac{E}{{R}_{��}}$�ļ��㣮

 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д� ��ͼ������A��B�������ֱ�Ϊ11N��7N�����Ƶ��ɳӡ�ϸ�ߵ�������һ��Ħ����������A��֧�����͵��ɳӵĶ���Ϊ��������
��ͼ������A��B�������ֱ�Ϊ11N��7N�����Ƶ��ɳӡ�ϸ�ߵ�������һ��Ħ����������A��֧�����͵��ɳӵĶ���Ϊ��������| A�� | 0N��7N | B�� | 4N��7N | C�� | 0N��18N | D�� | 4N��18N |
| A�� | �μ�ʮ���� | B�� | ǰ5���� | C�� | ��5��ĩ | D�� | ������ܾ��ˡ� |
 ��ͼ��ʾ��EΪ��أ�L�ǵ���ɺ��Բ��ơ��Ը�ϵ���㹻�����Ȧ��D1��D2�����������ͬ�Ҷ��ѹ�㹻��ĵ��ݣ�S�ǿ��Ƶ�·�Ŀ��أ����������·������˵����ȷ���ǣ�������
��ͼ��ʾ��EΪ��أ�L�ǵ���ɺ��Բ��ơ��Ը�ϵ���㹻�����Ȧ��D1��D2�����������ͬ�Ҷ��ѹ�㹻��ĵ��ݣ�S�ǿ��Ƶ�·�Ŀ��أ����������·������˵����ȷ���ǣ�������| A�� | �պϿ���S����·�ﵽ�ȶ����ٽ�S�Ͽ�˲�䣬D2����Ϩ��D1����һ����Ϩ�� | |
| B�� | �պϿ���S����·�ﵽ�ȶ���D1Ϩ��D2��ԭ������ | |
| C�� | �ձպϿ���S��˲�䣬ͨ��D1��D2�ĵ�����С��� | |
| D�� | �ձպϿ���S��˲�䣬ͨ��D1��D2�ĵ�����С����� |

| A�� | �ױ����ȳ��� | B�� | ���Ҵ�ͬһ�ط����� | ||
| C�� | ���˶�����С���ҵ��˶����� | D�� | �ij���������ǰ��X0�� |
 ��ͼ��ʾ������Ϊm����ΪL�Ľ�����MN�����ɵȳ������ʾ�Եϸ��ˮƽ���ң�������ֱ���ϵ���ǿ�ų��У�����ͨ����M��N�ĵ���ΪI��ƽ��ʱ����������ֱ����нǾ�Ϊ��=30�㣮
��ͼ��ʾ������Ϊm����ΪL�Ľ�����MN�����ɵȳ������ʾ�Եϸ��ˮƽ���ң�������ֱ���ϵ���ǿ�ų��У�����ͨ����M��N�ĵ���ΪI��ƽ��ʱ����������ֱ����нǾ�Ϊ��=30�㣮
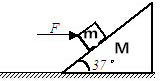 ��ͼ��ʾ������ΪM=5kg��б���壬����ˮƽ�����ϣ�б�������Ϊ37�㣬б���Ϸ�������Ϊm=3kg�����壬��ˮƽ��F�����壬����һ����ˮƽ��������ǰ����б����������Ķ�Ħ��������=0.2��ȡg=10m/s2��sin37��=0.6��cos37��=0.8����
��ͼ��ʾ������ΪM=5kg��б���壬����ˮƽ�����ϣ�б�������Ϊ37�㣬б���Ϸ�������Ϊm=3kg�����壬��ˮƽ��F�����壬����һ����ˮƽ��������ǰ����б����������Ķ�Ħ��������=0.2��ȡg=10m/s2��sin37��=0.6��cos37��=0.8����