题目内容
如图所示,已知绳长为L1=20 cm,水平杆L2=0.1 m,小球质量m=0.3 kg,整个装置可绕竖直轴转动,问:
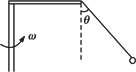
(1)要使绳子与竖直方向成45°角,试求该装置必须以多大的角速度转动才行?
(2)此时绳子的张力是多大?
答案:
解析:
解析:
|
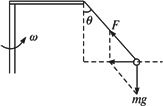
答案:(1)6.4 rad/s (2)4.24 N 解析:对小球受力分析如图所示,设绳对小球拉力为F,重力为mg,则绳的拉力与重力的合力提供小球做圆周运动的向心力.
对小球利用牛顿第二定律可得: mgtan45°=mω2r r=L2+Lsin45° 联立以上两式,将数值代入可得 ω=6.4 rad/s F= 思路分析:小球绕杆做圆周运动,其轨道平面在水平面内,轨道半径r=L2+Lsin45°,绳的拉力与重力的合力提供小球做圆周运动的向心力. |

练习册系列答案
相关题目
 “水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,则( )
“水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,则( )| A、小球运动到最低点Q时,处于失重状态 | ||
| B、小球初速度v0越大,则在P、Q两点绳对小球的拉力差越大 | ||
C、当v0>
| ||
D、当v0<
|
“水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,则 
| A.小球运动到最低点Q时,处于失重状态 |
| B.小球初速度v0越大,则在P、Q两点绳对小球的拉力差越大 |
C.当 时,小球一定能通过最高点P 时,小球一定能通过最高点P |
D.当 时,细绳始终处于绷紧状态 时,细绳始终处于绷紧状态 |
 ,小球质量m=0.3kg,整个装置可绕竖直轴转动,问:
,小球质量m=0.3kg,整个装置可绕竖直轴转动,问:




 时,小球一定能通过最高点P
时,小球一定能通过最高点P 时,细绳始终处于绷紧状态
时,细绳始终处于绷紧状态