题目内容
 电磁炮是一种理想的兵器,它的主要原理如图所示.1982年澳大利亚国立大学制成了能把m=2.2g的弹体(包括金属杆CD的质量)加速到v=10km/s的电磁炮.若轨道宽L=2m,长s=100m,通过的电流为I=10A,则
电磁炮是一种理想的兵器,它的主要原理如图所示.1982年澳大利亚国立大学制成了能把m=2.2g的弹体(包括金属杆CD的质量)加速到v=10km/s的电磁炮.若轨道宽L=2m,长s=100m,通过的电流为I=10A,则(1)轨道间所加的匀强磁场的磁感应强度为多少?
(2)磁场力的最大功率为多少(轨道摩擦不计)?
分析:(1)金属杆CD受到安培力作用,做加速运动,使弹体获得了速度,根据动能定理和安培力公式求解匀强磁场的磁感应强度.
(2)由于安培力大小一定,则当弹体(包括金属杆CD的质量)加速到v=10km/s时,磁场力功率最大,由P=Fv求出最大功率.
(2)由于安培力大小一定,则当弹体(包括金属杆CD的质量)加速到v=10km/s时,磁场力功率最大,由P=Fv求出最大功率.
解答:解:(1)金属杆CD(含弹体)受到安培力作用,做加速运动的过程中,由动能定理有
BLIs=
mv2
即 B=
=
T=55T
(2)当弹体(包括金属杆CD的质量)加速到v=10km/s时,磁场力功率最大,则磁场力的最大功率为
Pm=Fv=BLIV=55×2×10×10×103W=1.1×107W
答:(1)轨道间所加的匀强磁场的磁感应强度为为55T.
(2)磁场力的最大功率为1.1×107W.
BLIs=
| 1 |
| 2 |
即 B=
| mv2 |
| 2LIs |
| 2.2×10-3×(10×103)2 |
| 2×2×100×10 |
(2)当弹体(包括金属杆CD的质量)加速到v=10km/s时,磁场力功率最大,则磁场力的最大功率为
Pm=Fv=BLIV=55×2×10×10×103W=1.1×107W
答:(1)轨道间所加的匀强磁场的磁感应强度为为55T.
(2)磁场力的最大功率为1.1×107W.
点评:本题安培力是恒力,涉及到力空间的累积效应,运用动能定理研究是常用的思路.

练习册系列答案
相关题目
 电磁炮是一种理想的兵器,它的主要原理如图所示.1982年澳大利亚国立大学制成了能把m=2.2g的弹体(包括金属杆CD的质量)加速到v=10km/s的电磁炮.若轨道宽L=2m,长S=100m,通过的电流为I=10A,则轨道间所加的匀强磁场的磁感应强度B=
电磁炮是一种理想的兵器,它的主要原理如图所示.1982年澳大利亚国立大学制成了能把m=2.2g的弹体(包括金属杆CD的质量)加速到v=10km/s的电磁炮.若轨道宽L=2m,长S=100m,通过的电流为I=10A,则轨道间所加的匀强磁场的磁感应强度B= 电磁炮是一种理想的兵器,它的主要原理如图所示,1982年,澳大利亚国立大
电磁炮是一种理想的兵器,它的主要原理如图所示,1982年,澳大利亚国立大 电磁炮是一种理想的兵器,它的主要原理如图所示.1982年澳大利亚制成了能把2.2kg静止的弹体(包括金属杆EF的质量)加速到1.0×104m/s的电磁炮(常规炮弹的速度约为2ⅹ103m/s).若轨道宽为2m,长100m,通过的电流为10A,则轨道间所加匀强磁场的磁感强度为多大?磁场力的最大功率为多大?(轨道摩擦不计)
电磁炮是一种理想的兵器,它的主要原理如图所示.1982年澳大利亚制成了能把2.2kg静止的弹体(包括金属杆EF的质量)加速到1.0×104m/s的电磁炮(常规炮弹的速度约为2ⅹ103m/s).若轨道宽为2m,长100m,通过的电流为10A,则轨道间所加匀强磁场的磁感强度为多大?磁场力的最大功率为多大?(轨道摩擦不计)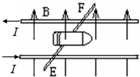 电磁炮是一种理想的兵器,它的主要原理如图所示.1982年澳大利亚国立大学制成了能把m=2.0g的弹体(包括金属杆EF的质量)加速到v=10km/s的电磁炮(常规炮弹的速度约为2km/s),若轨道宽L=2m,长为x=50m,通过的电流为I=10A,试问轨道间所加匀强磁场的磁感应强度和磁场的最大功率Pm有多大(轨道摩擦不计)?
电磁炮是一种理想的兵器,它的主要原理如图所示.1982年澳大利亚国立大学制成了能把m=2.0g的弹体(包括金属杆EF的质量)加速到v=10km/s的电磁炮(常规炮弹的速度约为2km/s),若轨道宽L=2m,长为x=50m,通过的电流为I=10A,试问轨道间所加匀强磁场的磁感应强度和磁场的最大功率Pm有多大(轨道摩擦不计)?