题目内容
如图所示,一直角三棱镜截面ABC,∠ABC=30°,∠ACB=90°斜边长为L,其折射率为n=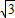 ,一束平行光从斜边距A点
,一束平行光从斜边距A点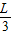 处的O点平行于BC边射入该棱镜.(光在真空中的速度c=3.0×108m/s,不考试光的反射.)
处的O点平行于BC边射入该棱镜.(光在真空中的速度c=3.0×108m/s,不考试光的反射.)①做出光的折射光路图,并求出光射出棱镜时光的偏向角;
②求出光在棱镜中传播的时间.
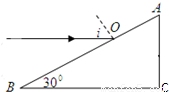
【答案】分析:①先由几何知识求出光线在AB面上的入射角,根据折射定律求出折射角,确定出光线在AC面上的入射角,由折射定律求出折射角,画出光路图,再由几何知识求解光射出棱镜时光的偏向角;
②由v=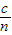 求出光在三棱镜中传播速度,由几何知识求出在介质中传播的路程s,由t=
求出光在三棱镜中传播速度,由几何知识求出在介质中传播的路程s,由t=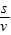 求出光在棱镜中传播的时间.
求出光在棱镜中传播的时间.
解答:解:①光路图如图所示.设光在AB面和AC面两次折射的入射角分别为i、i′,折射角分别为r、r′,由光的折射定律得: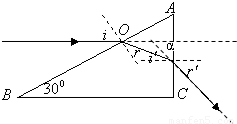
n=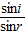 ,i=60°
,i=60°
可得:r=30°
由几何关系知:i′=30°
又n=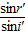
可得:r′=60°
所以光射出棱镜时光的偏向角为α=(i-i′)+(r′-i′)=60°.
②由于v=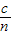
由几何知识得:光在介质中传播的路程为s=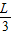
光在棱镜中传播的时间为t=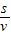
联立解得:t=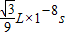
答:①做出光的折射光路图如图所示,光射出棱镜时光的偏向角是60°;
②光在棱镜中传播的时间是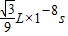 .
.
点评:能正确的作出光路图是解本题的关键,还要掌握折射定律的一些公式:n=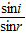 ,n=
,n=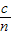 .此题属于中档题.
.此题属于中档题.
②由v=
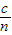 求出光在三棱镜中传播速度,由几何知识求出在介质中传播的路程s,由t=
求出光在三棱镜中传播速度,由几何知识求出在介质中传播的路程s,由t=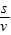 求出光在棱镜中传播的时间.
求出光在棱镜中传播的时间.解答:解:①光路图如图所示.设光在AB面和AC面两次折射的入射角分别为i、i′,折射角分别为r、r′,由光的折射定律得:

n=
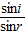 ,i=60°
,i=60°可得:r=30°
由几何关系知:i′=30°
又n=
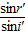
可得:r′=60°
所以光射出棱镜时光的偏向角为α=(i-i′)+(r′-i′)=60°.
②由于v=
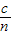
由几何知识得:光在介质中传播的路程为s=
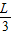
光在棱镜中传播的时间为t=
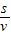
联立解得:t=
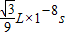
答:①做出光的折射光路图如图所示,光射出棱镜时光的偏向角是60°;
②光在棱镜中传播的时间是
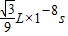 .
.点评:能正确的作出光路图是解本题的关键,还要掌握折射定律的一些公式:n=
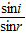 ,n=
,n=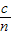 .此题属于中档题.
.此题属于中档题. 
练习册系列答案
相关题目
 如图所示,一个用透明材料制成的截面为直角三角形的三棱ABC,现在有一束单色光从空气中以θ1=45°的入射角自直角边 AB射入,折射时的偏向角为15°,然后光线射到AC面时刚好发生了全反射.求:
如图所示,一个用透明材料制成的截面为直角三角形的三棱ABC,现在有一束单色光从空气中以θ1=45°的入射角自直角边 AB射入,折射时的偏向角为15°,然后光线射到AC面时刚好发生了全反射.求: 由透明体做成的三棱柱,横截面为有一个锐角为30°的直角三角形,如图所示,AC面镀膜,经透明体射到AC面的光只能反射.现有一束光从AB面的D点垂直AB面射入透明体,经AC面E点反射后从BC面射出透明体,出射光线与BC面成30°角
由透明体做成的三棱柱,横截面为有一个锐角为30°的直角三角形,如图所示,AC面镀膜,经透明体射到AC面的光只能反射.现有一束光从AB面的D点垂直AB面射入透明体,经AC面E点反射后从BC面射出透明体,出射光线与BC面成30°角 如图所示,一直角三棱镜面ABC,∠ABC=30°,∠ACB=90°,斜边长为L,其折射率为n=
如图所示,一直角三棱镜面ABC,∠ABC=30°,∠ACB=90°,斜边长为L,其折射率为n=
