Question

在光滑绝缘水平面的P点正上方O点固定了一电荷量为+Q的正点电荷，在水平面上的N点，由静止释放质量为m，电荷量为—q的负检验电荷，该检验电荷经过P点时速度为v，图中θ=60°，规定电场中P点的电势为零．则在+Q形成的电场中：(   )

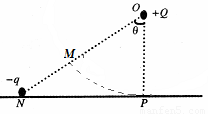
A．N点电势高于P点电势

B．P点电场强度大小是N点的2倍

C． N点电势为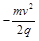

D．检验电荷在N点具有的电势能为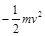

 

Answer 1

【答案】

D

【解析】

试题分析：（1）对物体进行受力分析，受重力、支持力、库仑力，根据竖直方向合力等于零，求出物体在A点受到轨道的支持力．

（2）从A点到B点，只有电场力做功，根据动能定理，求出电场力做功，从而得出两点间的电势差，从而得出B点的电势．

（3）当小球运动到无穷远处时，速度最大，根据能量守恒求出小球的最大速度．

解：（1）物体受到点电荷的库仑力F="kQq" r2

由几何关系可知 r="h" sin60°

设物体在A点时受到轨道的支持力大小为N，由平衡条件有

N-mg-Fsin60°=0

解得：N="mg+3" 3 kQq 8h2

（2）设点电荷产生的电场在B点的电势为φB，由动能定理有：

q(φ-φ B)="1" 2 mv2-1 2 mv02

解得φ B=φ+m(v02-v2) 2q

（3）设物块能获得的最大速度为vm，由能量守恒定律有：

qφ+1 2 mv02="1" 2 mvm2

解得vm= v02+2qφ m 

考点：动能定理的应用；库仑定律；电势．

点评：解决本题的关键知道电场力做功W=qU，U等于两点间的电势差．以及掌握库仑定律和动能定理的运用．