题目内容
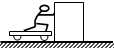
有某三棱镜的横截面是一直角三角形,如图6-20所示,∠A=90°,∠B=30°,∠C=60°,棱镜材料的折射率为n,底面BC涂黑,入射光沿平行于底面BC面,经AB面和AC面折射后出射.
图6-20
(1)求出射光线与入射光线延长线间的夹角δ.
(2)为使上述入射光线能从AC面出射,折射率n的最大值为多少?
解析:(1)入射角i=60°,由折射定律可得光线在AB面的折射角α,有:
sini=nsinα
sinα=![]() sin60°=
sin60°=![]()
在AC面的入射角β,有α+β=90°
sinβ=cosα=![]()
在AC面的折射角r,由折射定律:
nsinβ=sinr
sinr=n![]() =
=![]()
δ=r-30°=arcsin![]() -30°.
-30°.
(2)要使光从AC面出射,应有sinr≤1,即![]() ≤1,n≤
≤1,n≤![]() .
.
答案:(1)δ=arcsin![]() -30° (2)
-30° (2)![]()

练习册系列答案
相关题目
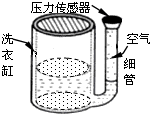 (1)当洗衣缸内水位缓慢升高时,设细管内空气温度不变,
(1)当洗衣缸内水位缓慢升高时,设细管内空气温度不变,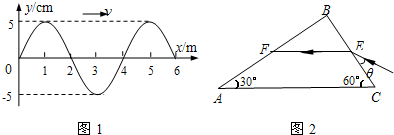
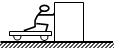 A.男孩和木箱组成的系统动量守恒
A.男孩和木箱组成的系统动量守恒
 列波的波速.
列波的波速.

 m,水池里装有高度为
m,水池里装有高度为 m、折射率为
m、折射率为 的某种液体,在水池底部水平放置宽度d'=5m的平面镜,水池左壁高
的某种液体,在水池底部水平放置宽度d'=5m的平面镜,水池左壁高 m处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,不考虑光在水池面上的反射,求在此横截面上标尺上被照亮的长度和液面上能射出光线部分的长度.
m处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,不考虑光在水池面上的反射,求在此横截面上标尺上被照亮的长度和液面上能射出光线部分的长度.
