题目内容
如图甲所示，质量为 1.0kg的物体置于固定斜面上，斜面的倾角 θ=30°，对物体施以平行于斜面向上的拉力 F，1.0 s 后将拉力撤去，物体运动的 v-t图象如图乙（设斜向上为正，g=10m/s2 ），试求：（1）拉力 F 的大小；
（2）物块与斜面的动摩擦因数为 μ．
【答案】分析：由速度的斜率求出加速度，根据牛顿第二定律分别对拉力撤去前、后过程列式，可拉力和物块与斜面的动摩擦因数为 μ．
解答：解：由图象得：拉力撤去前物体的加速度大小为 a1=
；撤去拉力后的加速度大小为 a2=
，根据牛顿第二定律得：
拉力撤去前：F-mgsinθ-μmgcosθ=ma1 ①
拉力撤去后：mgsinθ+μmgcosθ=ma2 ②
由②得：μ=
=
=
代入①解得，F=18N
答：
（1）拉力 F 的大小是18N；
（2）物块与斜面的动摩擦因数为=
．
点评：本题首先挖掘速度图象的物理意义，由斜率求出加速度，其次求得加速度后，由牛顿第二定律求解物体的受力情况．
解答：解：由图象得：拉力撤去前物体的加速度大小为 a1=
；撤去拉力后的加速度大小为 a2=，根据牛顿第二定律得：拉力撤去前：F-mgsinθ-μmgcosθ=ma1 ①
拉力撤去后：mgsinθ+μmgcosθ=ma2 ②
由②得：μ=
==代入①解得，F=18N
答：
（1）拉力 F 的大小是18N；
（2）物块与斜面的动摩擦因数为=
．点评：本题首先挖掘速度图象的物理意义，由斜率求出加速度，其次求得加速度后，由牛顿第二定律求解物体的受力情况．
练习册系列答案
名校课堂系列答案
相关题目
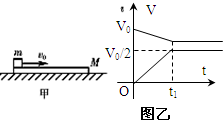如图甲所示，质量为M的木板静止在光滑水平面上，一个质量为m的小滑块以初速度υ0从木板的左端向右滑上木板．滑块和木板速度随时间变化的图象如图乙所示，某同学根据图象作出如下一些判断，正确的是（ ）?
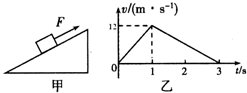如图甲所示，质量为 1.0kg的物体置于固定斜面上，斜面的倾角 θ=30°，对物体施以平行于斜面向上的拉力 F，t=1.0s后将拉力撤去，物体运动的 v-t图象如图乙（设斜向上为正，g=10m/s2 ），试求：
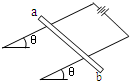如图甲所示，质量为m的细杆ab置于倾角为θ的导轨上，ab处于磁场中，ab与导轨间动摩擦因数为μ，有电流时，ab恰好静止在导轨上，则从b端的侧视图看，其中杆 ab与导轨间摩擦力可能为“0”的是（ ）
一有界匀强磁场区域如图甲所示，质量为m、电阻为R的长方形矩形线圈abcd边长分别为L和2L，线圈一半在磁场内，一半在磁场外，磁感应强度为B0，t=0时刻磁场开始均匀减小，线圈中产生感应电流，在磁场力作用下运动，v-t图象如图乙，图中斜向虚线为过O点速度图线的切线，数据由图中给出，不考虑重力影响，则磁场磁感应强度的变化率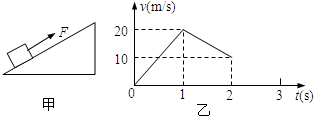
（2009?广东模拟）如图甲所示，质量为m=1kg的物体置于倾角θ=37°的固定粗糙斜面上．对物体施以平行于斜面向上的拉力F，t1=1s时撤去拉力，物体运动的部分v-t图象如图乙所示，则下列说法中正确的是：（g=10m/s2）（ ）