题目内容
回旋加速器英文:Cyclotron 它是利用磁场使带电粒子作回旋运动,在运动中经高频电场反复加速的装置,是高能物理中的重要仪器.
1930年Earnest O.Lawrence提出回旋加速器的理论,1932年首次研制成功.它的主要结构是在磁极间的真空室内有两个半圆形的金属扁盒(D形盒)隔开相对放置,D形盒上加交变电压,其间隙处产生交变电场.在D形盒所在处存在磁感应强度为B的匀强磁场.置于中心的粒子源产生的带电粒子,质量为m,电荷量为q,在电场中被加速,带电粒子在D形盒内不受电场力,在洛伦兹力作用下,在垂直磁场平面内作圆周运动.如果D形盒上所加的交变电压的频率恰好等于粒子在磁场中作圆周运动的频率,则粒子绕行半圈后正赶上D形盒上极性变号,粒子仍处于加速状态.由于上述粒子绕行半圈的时间与粒子的速度无关,因此粒子每绕行半圈受到一次加速,绕行半径增大.经过很多次加速,粒子沿如图2所示的轨迹从D形盒边缘引出,能量可达几十兆电子伏特(MeV ).回旋加速器的能量受制于随粒子速度增大的相对论效应,粒子的质量增大,粒子绕行周期变长,从而逐渐偏离了交变电场的加速状态.
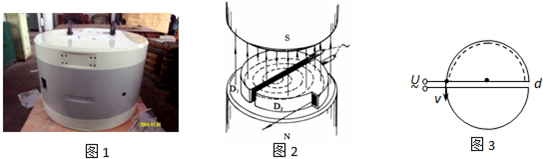
图1是回旋加速器的实物图,图2、图3是回旋加速器的原理图,一质量为m,电荷量为q的带电粒子自半径为R的D形盒的中心由静止开始加速,D形盒上加交变电压大小恒为U,两D形盒之间的距离为d,D形盒所在处的磁场的磁感应强度为B,不考虑相对论效应,求:
(1)带电粒子被第一次加速后获得的速度v1;
(2)带电粒子加速后获得的最大速度vm;
(3)带电粒子由静止开始到第n次加速结束时在电场和磁场中运动所用的总时间是多少?若要增大带电粒子加速后获得的最大速度vm,你认为可以采取哪些方案?
1930年Earnest O.Lawrence提出回旋加速器的理论,1932年首次研制成功.它的主要结构是在磁极间的真空室内有两个半圆形的金属扁盒(D形盒)隔开相对放置,D形盒上加交变电压,其间隙处产生交变电场.在D形盒所在处存在磁感应强度为B的匀强磁场.置于中心的粒子源产生的带电粒子,质量为m,电荷量为q,在电场中被加速,带电粒子在D形盒内不受电场力,在洛伦兹力作用下,在垂直磁场平面内作圆周运动.如果D形盒上所加的交变电压的频率恰好等于粒子在磁场中作圆周运动的频率,则粒子绕行半圈后正赶上D形盒上极性变号,粒子仍处于加速状态.由于上述粒子绕行半圈的时间与粒子的速度无关,因此粒子每绕行半圈受到一次加速,绕行半径增大.经过很多次加速,粒子沿如图2所示的轨迹从D形盒边缘引出,能量可达几十兆电子伏特(MeV ).回旋加速器的能量受制于随粒子速度增大的相对论效应,粒子的质量增大,粒子绕行周期变长,从而逐渐偏离了交变电场的加速状态.

图1是回旋加速器的实物图,图2、图3是回旋加速器的原理图,一质量为m,电荷量为q的带电粒子自半径为R的D形盒的中心由静止开始加速,D形盒上加交变电压大小恒为U,两D形盒之间的距离为d,D形盒所在处的磁场的磁感应强度为B,不考虑相对论效应,求:
(1)带电粒子被第一次加速后获得的速度v1;
(2)带电粒子加速后获得的最大速度vm;
(3)带电粒子由静止开始到第n次加速结束时在电场和磁场中运动所用的总时间是多少?若要增大带电粒子加速后获得的最大速度vm,你认为可以采取哪些方案?
分析:(1)根据动能定理求出粒子被第一次加速后获得的速度.
(2)当粒子从D形盒出来时,此时在磁场中运动的半径最大,速度最大,根据洛伦兹力提供向心力,运用牛顿第二定律求出粒子的最大速度.
(3)分别求出粒子在电场中加速的时间和在磁场中运动的时间,从而求出总时间.通过第(2)问求出的粒子最大速度,看最大速度与什么因素有关,从而确定改变的方案.
(2)当粒子从D形盒出来时,此时在磁场中运动的半径最大,速度最大,根据洛伦兹力提供向心力,运用牛顿第二定律求出粒子的最大速度.
(3)分别求出粒子在电场中加速的时间和在磁场中运动的时间,从而求出总时间.通过第(2)问求出的粒子最大速度,看最大速度与什么因素有关,从而确定改变的方案.
解答:解:(1)根据动能定理得,
Uq=
m
∴v1=
(2)当粒子从D形盒中出来时速度最大,根据牛顿第二定律得,
q
B=m
∴vm=
(3)根据牛顿第二定律得,
qvB=m
∴r=
粒子在磁场中运动的周期
T=
=
粒子在电场中一直做匀加速直线运动,有:
带电粒子由静止开始到第n次加速,在磁场中运动的时间:
t磁=(n-1)
=(n-1)
则粒子在电场和磁场中运动的总时间:
t总=t电+t磁=d
+(n-1)
根据q
B=m
∴vm=
知方案1:增大磁场的磁感应强度B
方案2:增大D型盒的半径R
答:(1)带电粒子被第一次加速后获得的速度为
.
(2)带电粒子加速后获得的最大速度为
.
(3)带电粒子由静止开始到第n次加速结束时在电场和磁场中运动所用的总时间是d
+(n-1)
.若要增大带电粒子加速后获得的最大速度vm,可以增大磁感应强度或增大D形盒的半径.
Uq=
| 1 |
| 2 |
| v | 2 1 |
|
(2)当粒子从D形盒中出来时速度最大,根据牛顿第二定律得,
q
| v | m |
|
| qBR |
| m |
(3)根据牛顿第二定律得,
qvB=m
|
| mv |
| qB |
粒子在磁场中运动的周期
T=
| 2π r |
| v |
| 2π | ||
| qB |
粒子在电场中一直做匀加速直线运动,有:
|
带电粒子由静止开始到第n次加速,在磁场中运动的时间:
t磁=(n-1)
| T |
| 2 |
| π m |
| qB |
则粒子在电场和磁场中运动的总时间:
t总=t电+t磁=d
|
| π m |
| qB |
根据q
| v | m |
|
| qBR |
| m |
知方案1:增大磁场的磁感应强度B
方案2:增大D型盒的半径R
答:(1)带电粒子被第一次加速后获得的速度为
|
(2)带电粒子加速后获得的最大速度为
| qBR |
| m |
(3)带电粒子由静止开始到第n次加速结束时在电场和磁场中运动所用的总时间是d
|
| π m |
| qB |
点评:解决本题的关键知道回旋加速器加速粒子的原理,运用电场加速和磁场偏转进行,注意最终的最大速度与加速的电压无关.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
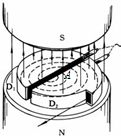 2006年6月23日,中国首台西门子eclipse HP/RD医用回旋加速器在位于广州军区总医院内的正电子药物研发中心正式投入临床运营.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U.加速过程中不考虑重力作用.( )
2006年6月23日,中国首台西门子eclipse HP/RD医用回旋加速器在位于广州军区总医院内的正电子药物研发中心正式投入临床运营.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U.加速过程中不考虑重力作用.( )A、某粒子第1次和第2次经过两狭缝后的轨道半径之比为1:
| ||
B、粒子从静止开始加速到出口处所需的时间为
| ||
| C、粒子能获得的最大动能Ek加速器磁感应强度无关 | ||
| D、加速电压越大粒子能获得的最大动能Ek大 |
在回旋加速器中,下列说法正确的是( )
| A、电场用来加速带电粒子,磁场使带电粒子偏转 | B、电场和磁场同时用来加速带电粒子 | C、在确定的交流电压下,回旋加速器D形金属盒内的磁场越强,同一带电粒子获得的动能就越大 | D、同一带电粒子获得的最大动能只与交流电源的电压有关,而与交流电的频率无 |
 回旋加速器以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为d,两侧为相同匀强磁场,方向垂直纸面向里.一质量m电量+q的带电粒子,以初速度V1垂直边界射入磁场做匀速圆周运动,再进入电场做匀加速运动,后第二次进入磁场中运动…,粒子在电场和磁场中不断交替运动.已知粒子第二次在磁场中运动半径是第一次的二倍,第三次是第一次的三倍,…以此类推.则( )
回旋加速器以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为d,两侧为相同匀强磁场,方向垂直纸面向里.一质量m电量+q的带电粒子,以初速度V1垂直边界射入磁场做匀速圆周运动,再进入电场做匀加速运动,后第二次进入磁场中运动…,粒子在电场和磁场中不断交替运动.已知粒子第二次在磁场中运动半径是第一次的二倍,第三次是第一次的三倍,…以此类推.则( )