题目内容
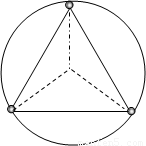
宇宙中存在一些离其他恒星较远的，由质量相等的三颗星组成的三星系统，通常可忽略其他星体对他们的引力作用。 已观测到稳定的三星系统存在的一种形式是三颗星位于等边三角形三个项点上，并沿外接于等边三角形的圆形轨道运行。设每个星体的质量均为m，相邻的两颗星之间的距离为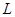
，引力常量为
，求：
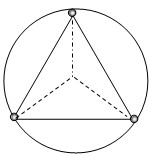
（1）该圆形轨道的半径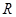
为多少？
（2）星体的运行周期为多少？
【答案】
【解析】
试题分析：（1）由几何关系得：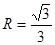
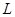（2分）
（2）由万有引力定律和牛顿运动定律得：
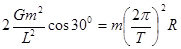（4分）
由上式可得：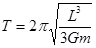
（2分）
考点：考查了万有引力定律的应用
点评：解决本题的关键知道行星做圆周运动向心力的来源，以及会通过几何关系求出做圆周运动的轨道半径．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
宇宙中存在一些离其他恒星较远的、由两颗星体组成双星系统．它们的简化模型如图所示，假设两个天体（可视为质点）绕它们连线上的O点做匀速圆周运动，它们之间的距离为L，其中天体A的质量为m1，天体B的质量为m2．A到O的距离是r，转动的角速度为ω．则下列说法正确的是（ ）
宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其他星体对它们的引力作用，已观测到稳定的三星系统存在形式之一是：三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行，设每个星体的质量均为M，则（ ）
恒星系统或恒星系是少数几颗恒星受到引力的拘束而互相环绕的系统，宇宙中存在一些离其他恒星很远的四颗星组成的四星系统，通常可忽略很远的其他星体对它们的引力作用，稳定的四星系统存在的一种基本的构成形式是四颗质量相等的星位于正方形的四个顶点上，沿外接于正方形的圆形轨道运行，如图所示．若已知每颗星质量均为m，正方形边长为L，万有引力常量为G，求：