题目内容
5.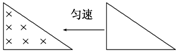 如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场,磁场仅限于三角形边界所围的区域内,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一条直线上.若取顺时针方向为电流的正方向,则金属框穿过磁场过程的感应电流i随时间t变化的图象是下图所示的( )
如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场,磁场仅限于三角形边界所围的区域内,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一条直线上.若取顺时针方向为电流的正方向,则金属框穿过磁场过程的感应电流i随时间t变化的图象是下图所示的( )| A. |  | B. |  | C. |  | D. |  |
分析 先根据楞次定律判断感应电流的方向.再由E=BLv,分析感应电动势,其中L是有效的切割长度.由欧姆定律得到感应电流与时间的关系式.
解答 解:设直角三角形右下角为α.
金属框进入磁场的过程,感应电动势为 E=BLv,L=vttanα,则得 E=Bv2t•tanα,感应电流大小:i=$\frac{E}{R}$∝t,
由楞次定律判断得知:感应电流为逆时针方向,是负值;
金属框穿出磁场的过程,感应电动势为:E=BLv,L=[L0-v(t-$\frac{{L}_{0}}{v}$)]tanα=(2L0-vt)tanα
L0是三角形底边的长度,则得:
E=B(2L0-vt)v•tanα,
感应电流大小:i=$\frac{E}{R}=\frac{B(2{L}_{0}-vt)vtanα}{R}$,由楞次定律判断得知:感应电流为顺时针方向,是正值;由数学知识可知C图象正确.
故选:C.
点评 本题是楞次定律和法拉第电磁定律、欧姆定律的综合应用,分段得到电流的表达式,再选择图象.

练习册系列答案
相关题目
15. 如图所示,a、b、c、d为导体圆环的四等分点,圆环的半径为R,一匀强磁场垂直于圆环平面,且磁场的磁感应强度随时间变化规律满足B=kt,则a、b两点间的电压为( )
如图所示,a、b、c、d为导体圆环的四等分点,圆环的半径为R,一匀强磁场垂直于圆环平面,且磁场的磁感应强度随时间变化规律满足B=kt,则a、b两点间的电压为( )
 如图所示,a、b、c、d为导体圆环的四等分点,圆环的半径为R,一匀强磁场垂直于圆环平面,且磁场的磁感应强度随时间变化规律满足B=kt,则a、b两点间的电压为( )
如图所示,a、b、c、d为导体圆环的四等分点,圆环的半径为R,一匀强磁场垂直于圆环平面,且磁场的磁感应强度随时间变化规律满足B=kt,则a、b两点间的电压为( )| A. | 0 | B. | $\frac{{πk{R^2}}}{4}$ | C. | $\frac{{3πk{R^2}}}{4}$ | D. | πkR2 |
16. 如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆角速度为ω1时,小球旋转平面在A处,球对杆的压力为FN1;当杆角速度为ω2时,小球旋转平面在B处,球对杆的压力为FN2,则有( )
如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆角速度为ω1时,小球旋转平面在A处,球对杆的压力为FN1;当杆角速度为ω2时,小球旋转平面在B处,球对杆的压力为FN2,则有( )
 如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆角速度为ω1时,小球旋转平面在A处,球对杆的压力为FN1;当杆角速度为ω2时,小球旋转平面在B处,球对杆的压力为FN2,则有( )
如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆角速度为ω1时,小球旋转平面在A处,球对杆的压力为FN1;当杆角速度为ω2时,小球旋转平面在B处,球对杆的压力为FN2,则有( )| A. | FN1>FN2 | B. | FN1=FN2 | C. | ω1<ω2 | D. | ω1>ω2 |
20.各行星的运动近似看作匀速圆周运动,则离太阳越远的行星( )
| A. | 周期越小 | B. | 线速度越小 | C. | 角速度越大 | D. | 向心加速度越小 |
17.质量为m的物体,在水平力F作用下,在粗糙的水平面上向右运动.如图所示,下列说法正确的是( )

| A. | 如果物体做匀速直线运动,F一定对物体不做功 | |
| B. | 如果物体做减速直线运动,F一定对物体做负功 | |
| C. | 如果物体做减速直线运动,F一定对物体做正功 | |
| D. | 如果物体做匀速直线运动,合力一定对物体做正功 |
14. 某介质中形成一列简谐波t=0时刻的波形如图中实线所示,若波向右传播,零时刻波刚好传到坐标位置为1m处的A点,且再经过0.7s,坐标7m处的P点第一次通过平衡位置并向上振动,则下列说法正确的是( )
某介质中形成一列简谐波t=0时刻的波形如图中实线所示,若波向右传播,零时刻波刚好传到坐标位置为1m处的A点,且再经过0.7s,坐标7m处的P点第一次通过平衡位置并向上振动,则下列说法正确的是( )
 某介质中形成一列简谐波t=0时刻的波形如图中实线所示,若波向右传播,零时刻波刚好传到坐标位置为1m处的A点,且再经过0.7s,坐标7m处的P点第一次通过平衡位置并向上振动,则下列说法正确的是( )
某介质中形成一列简谐波t=0时刻的波形如图中实线所示,若波向右传播,零时刻波刚好传到坐标位置为1m处的A点,且再经过0.7s,坐标7m处的P点第一次通过平衡位置并向上振动,则下列说法正确的是( )| A. | 该列波的传播速度为$\frac{60}{7}$m/s | |
| B. | 这列波的周期为$\frac{7}{30}$s | |
| C. | 从t=0时刻其到P点第一次达到波峰停止,O点对平衡位置的位移y0=-2cm | |
| D. | 从t=0时刻起到P点的第一次到达波峰时止,O点所经过的路程S0=0.3m | |
| E. | 该波遇到的频率为5Hz的机械波可发生干涉现象 |
15. 如图所示,离地面高h处有甲、乙两个物体,甲以初速度v0水平射出,同时乙以初速度v0沿倾角为30°的光滑斜面滑下.若甲到达地面的同时乙恰好运动到斜面的中点处,则v0的大小是( )
如图所示,离地面高h处有甲、乙两个物体,甲以初速度v0水平射出,同时乙以初速度v0沿倾角为30°的光滑斜面滑下.若甲到达地面的同时乙恰好运动到斜面的中点处,则v0的大小是( )
 如图所示,离地面高h处有甲、乙两个物体,甲以初速度v0水平射出,同时乙以初速度v0沿倾角为30°的光滑斜面滑下.若甲到达地面的同时乙恰好运动到斜面的中点处,则v0的大小是( )
如图所示,离地面高h处有甲、乙两个物体,甲以初速度v0水平射出,同时乙以初速度v0沿倾角为30°的光滑斜面滑下.若甲到达地面的同时乙恰好运动到斜面的中点处,则v0的大小是( )| A. | $\frac{\sqrt{2gh}}{2}$ | B. | $\frac{\sqrt{gh}}{4}$ | C. | $\frac{\sqrt{2gh}}{4}$ | D. | $\sqrt{2gh}$ |

 如图甲所示,截面积为0.2m2的100匝圆形线圈A处在变化的磁场中.磁场方向垂直纸面,其磁感应强度B随时间t的变化规律如图乙所示,设向外为B的正方向.R1=4Ω,R2=6Ω,线圈的内阻不计,
如图甲所示,截面积为0.2m2的100匝圆形线圈A处在变化的磁场中.磁场方向垂直纸面,其磁感应强度B随时间t的变化规律如图乙所示,设向外为B的正方向.R1=4Ω,R2=6Ω,线圈的内阻不计,