题目内容
10. 如图所示,间距为l的平行导轨MN、PQ与水平面夹角为α,导轨上端接电阻R,导轨处于匀强磁场中,磁场方向与导轨平面垂直,磁感应强度大小为B.现有一质量为m,长度也为l的导体棒从导轨上端释放,当下滑速率为v时,导体棒恰好能沿导轨做匀速运动;如果导体棒从导轨下端以初速度v沿导轨向上滑出后,导体棒沿导轨向上运动的最大距离为L.已知导体棒及导轨电阻忽略不计,运动过程中与导轨接触良好,重力加速度为g,请计算导体棒与导轨间的动摩擦因数以及导体棒上滑过程中电阻R产生的焦耳热.
如图所示,间距为l的平行导轨MN、PQ与水平面夹角为α,导轨上端接电阻R,导轨处于匀强磁场中,磁场方向与导轨平面垂直,磁感应强度大小为B.现有一质量为m,长度也为l的导体棒从导轨上端释放,当下滑速率为v时,导体棒恰好能沿导轨做匀速运动;如果导体棒从导轨下端以初速度v沿导轨向上滑出后,导体棒沿导轨向上运动的最大距离为L.已知导体棒及导轨电阻忽略不计,运动过程中与导轨接触良好,重力加速度为g,请计算导体棒与导轨间的动摩擦因数以及导体棒上滑过程中电阻R产生的焦耳热.
分析 根据共点力的平衡条件结合法拉第电磁感应定律、闭合电路的欧姆定律求解动摩擦因数;根据功能关系求解导体棒上滑过程中电阻R产生的焦耳热.
解答 解:导体棒下滑过程中达到最大速率v时产生的感应电动势为E=Blv,
根据闭合电路的欧姆定律可得感应电流I=$\frac{E}{R}=\frac{Blv}{R}$,
根据平衡条件可得:mgsinα=μmgcosα+BIl,
联立解得动摩擦因数为:μ=tanα-$\frac{{B}^{2}{l}^{2}v}{mgRcosα}$;
设导体棒上滑过程中电阻R上产生的焦耳热为Q,根据能量关系可得:
Q=$\frac{1}{2}m{v}^{2}-mgLsinα-μmgLcosα$,
所以得Q=$\frac{1}{2}m{v}^{2}+\frac{{B}^{2}{l}^{2}vL}{R}-2mgLsinα$.
答:导体棒与导轨间的动摩擦因数为tanα-$\frac{{B}^{2}{l}^{2}v}{mgRcosα}$;导体棒上滑过程中电阻R产生的焦耳热为$\frac{1}{2}m{v}^{2}+\frac{{B}^{2}{l}^{2}vL}{R}-2mgLsinα$.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

练习册系列答案
相关题目
20.下列一些说法中不正确的有( )
| A. | 产生离心现象的原理有时可利用为人类服务 | |
| B. | 汽车转弯时要利用离心现象防止事故 | |
| C. | 汽车转弯时要防止离心现象的发生,避免事故发生 | |
| D. | 洗衣机脱水桶脱干衣服利用的是离心现象 |
1. 如图所示,木块B上表面是水平的,木块A置于B上,一起以某一初速度沿光滑斜面向上冲,上冲过程中A与B保持相对静止,在向上运动的过程中( )
如图所示,木块B上表面是水平的,木块A置于B上,一起以某一初速度沿光滑斜面向上冲,上冲过程中A与B保持相对静止,在向上运动的过程中( )
 如图所示,木块B上表面是水平的,木块A置于B上,一起以某一初速度沿光滑斜面向上冲,上冲过程中A与B保持相对静止,在向上运动的过程中( )
如图所示,木块B上表面是水平的,木块A置于B上,一起以某一初速度沿光滑斜面向上冲,上冲过程中A与B保持相对静止,在向上运动的过程中( )| A. | 因AB的运动情况相同所以相互间没有摩擦力 | |
| B. | 木块A处于超重状态 | |
| C. | A的机械能不发生变化 | |
| D. | A对B做负功 |
18.下列说法中正确的是( )
| A. | 拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片以增加透射光的强度 | |
| B. | X射线能够穿透物质,可以用来检查人体内部器官 | |
| C. | 当波源与观察者互相靠近时,观察者接收到的波的频率会变小 | |
| D. | 第四代移动通信系统(4G)采用1 880~2 690 MHz间的四个频段,该电磁波信号的磁感应强度随时间是均匀变化的 |
15. 如图所示为某电场中的一条电场线,在a点静止地放一个正电荷(重力不能忽略),到达b时速度恰好为零,则( )
如图所示为某电场中的一条电场线,在a点静止地放一个正电荷(重力不能忽略),到达b时速度恰好为零,则( )
 如图所示为某电场中的一条电场线,在a点静止地放一个正电荷(重力不能忽略),到达b时速度恰好为零,则( )
如图所示为某电场中的一条电场线,在a点静止地放一个正电荷(重力不能忽略),到达b时速度恰好为零,则( )| A. | 电场线的方向一定竖直向上 | |
| B. | 该电场一定是匀强电场 | |
| C. | 该电荷从a→b是加速度变化的运动 | |
| D. | 该电荷在a点受到的电场力一定比在b点受到的电场力小 |
20.下列说法正确的是( )
| A. | 在光电效应实验中,遏止电压与入射光频率无关 | |
| B. | 比结合能越小,表示原子核中核子结合得越牢固,原子核越稳定 | |
| C. | 一个氢原子从n=3的物体发生跃迁,可能只辐射一种频率的光子 | |
| D. | 核力是强相互作用的一种表现,原子核尺度内,核力比库仑力小 |
 如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为l,两导轨间连有一电阻R,导轨平面与水平面的夹角为θ,在两虚线间的导轨上涂有薄绝缘涂层,涂层宽度也为l.匀强磁场的磁感应强度大小为B,方向与导轨平面垂直.质量为m的导体棒从h高度处由静止释放,在刚要滑到涂层处时恰好匀速运动.导体棒始终与导轨垂直且仅与涂层间有摩擦,动摩擦因数μ=tanθ,其他部分的电阻不计,重力加速度为g,求:
如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为l,两导轨间连有一电阻R,导轨平面与水平面的夹角为θ,在两虚线间的导轨上涂有薄绝缘涂层,涂层宽度也为l.匀强磁场的磁感应强度大小为B,方向与导轨平面垂直.质量为m的导体棒从h高度处由静止释放,在刚要滑到涂层处时恰好匀速运动.导体棒始终与导轨垂直且仅与涂层间有摩擦,动摩擦因数μ=tanθ,其他部分的电阻不计,重力加速度为g,求: 我们通过实验可以探究感应电流的产生条件,在下图的实验中,线圈A通过滑动变阻器和开关接到电源上,线圈B的两端连接到电流表上,把线圈A装在线圈B里面.通过实验,判断线圈B中是否有电流产生.
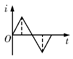
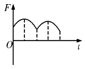
我们通过实验可以探究感应电流的产生条件,在下图的实验中,线圈A通过滑动变阻器和开关接到电源上,线圈B的两端连接到电流表上,把线圈A装在线圈B里面.通过实验,判断线圈B中是否有电流产生.  如图所示,xOy平面位于光滑水平桌面上,在O≤x≤2L的区域内存在着匀强磁场,磁场方向垂直于xOy平面向下.由同种材料制成的粗细均匀的正六边形导线框,放在该水平桌面上,AB与DE边距离恰为2L,现施加一水平向右的拉力F拉着线框水平向右匀速运动,DE边与y轴始终平行,从线框DE边刚进入磁场开始计时,则线框中的感应电流i(取逆时针方向的电流为正)随时间t的函数图象和拉力F随时间t的函数图象大致是( )
如图所示,xOy平面位于光滑水平桌面上,在O≤x≤2L的区域内存在着匀强磁场,磁场方向垂直于xOy平面向下.由同种材料制成的粗细均匀的正六边形导线框,放在该水平桌面上,AB与DE边距离恰为2L,现施加一水平向右的拉力F拉着线框水平向右匀速运动,DE边与y轴始终平行,从线框DE边刚进入磁场开始计时,则线框中的感应电流i(取逆时针方向的电流为正)随时间t的函数图象和拉力F随时间t的函数图象大致是( )