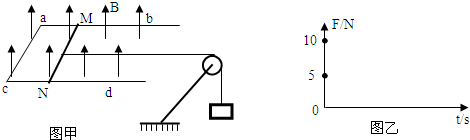
题目内容
如图甲所示，空间存在着一个范围足够大的竖直向下的匀强磁场，磁场的磁感强度大小为B．边长为l的正方形金属框abcd（下简称方框）放在光滑的水平地面上，其外侧套着一个与方框边长相同的U形金属框架MNPQ（下简称U形框），U形框与方框之间接触良好且无摩擦．两个金属框每条边的质量均为m，每条边的电阻均为r．（1）将方框固定不动，用力拉动U形框使它以速度v垂直NP边向右匀速运动，当U形框的MQ端滑至方框的最右侧（如图乙所示）时，方框上的bc两端的电势差为多大？此时方框的热功率为多大？
（2）若方框不固定，给U形框垂直NP边向右的初速度v，如果U形框恰好不能与方框分离，则在这一过程中两框架上产生的总热量为多少？
（3）若方框不固定，给U形框垂直NP边向右的初速度v（v＞v），U形框最终将与方框分离．如果从U形框和方框不再接触开始，经过时间t方框最右侧和U形框最左侧距离为s．求两金属框分离后的速度各多大．
【答案】分析：（1）U型框向右做切割磁感线运动，由E=BLv、欧姆定律求感应电流的大小．NP相当于电源，bc与ad组成一个并联的外电路，即可由欧姆定律和公式P=
求方框的热功率．
（2）若方框不固定，方框也向右运动，先做加速度减小的加速运动，U形框恰好不能与方框分离，两者速度相等而后做匀速运动，整体所受的合力为零，根据动量守恒求出共同速度，再由能量守恒求热量．
（3）从U形框和方框不再接触，两者都做匀速运动．设分离时，U形框速度为v1，方框速度为v2，根据动量守恒和运动学公式列式求两金属框分离后的速度．
解答：解：（1）U形框右边产生感应电动势：E=BLv0 ①
方框总电阻：
②
总电流：
③
bc两端电势差：U=IR ④
由以上各式解得：
⑤
方框热功率：
⑥
（2）U形框恰好不能与方框分离，两者速度相等，设共同速度为v，由动量守恒定律，有：3mv=（3m+4m）v ⑦
据能量转化与守恒，可知：
⑧
解得：
⑨
（3）设分离时，U形框速度为v1，方框速度为v2，由动量守恒可知：3mv=3mv1+4mv2 ⑩
从U形框和方框不再接触后，都做匀速运动，则有 s=v1t-v2t （11）
解得：
（12）
（13）
答：
（1）方框上的bc两端的电势差为
，此时方框的热功率为
．
（2）这一过程中两框架上产生的总热量为
．
（3）两金属框分离后的速度分别为
+
，
-
．
点评：本题是电磁感应与电路、力学知识的综合，关键要判断出线框的受力情况和运动情况，会根据法拉第定律、欧姆定律、动量守恒定律等等知识结合进行求解．
求方框的热功率．（2）若方框不固定，方框也向右运动，先做加速度减小的加速运动，U形框恰好不能与方框分离，两者速度相等而后做匀速运动，整体所受的合力为零，根据动量守恒求出共同速度，再由能量守恒求热量．
（3）从U形框和方框不再接触，两者都做匀速运动．设分离时，U形框速度为v1，方框速度为v2，根据动量守恒和运动学公式列式求两金属框分离后的速度．
解答：解：（1）U形框右边产生感应电动势：E=BLv0 ①
方框总电阻：
②总电流：
③bc两端电势差：U=IR ④
由以上各式解得：
⑤方框热功率：
⑥（2）U形框恰好不能与方框分离，两者速度相等，设共同速度为v，由动量守恒定律，有：3mv=（3m+4m）v ⑦
据能量转化与守恒，可知：
⑧解得：
⑨（3）设分离时，U形框速度为v1，方框速度为v2，由动量守恒可知：3mv=3mv1+4mv2 ⑩
从U形框和方框不再接触后，都做匀速运动，则有 s=v1t-v2t （11）
解得：
（12） （13）答：
（1）方框上的bc两端的电势差为
，此时方框的热功率为．（2）这一过程中两框架上产生的总热量为
．（3）两金属框分离后的速度分别为
+，-．点评：本题是电磁感应与电路、力学知识的综合，关键要判断出线框的受力情况和运动情况，会根据法拉第定律、欧姆定律、动量守恒定律等等知识结合进行求解．
练习册系列答案
相关题目
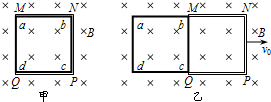（2006?泰州模拟）如图甲所示，空间存在着一个范围足够大的竖直向下的匀强磁场，磁场的磁感强度大小为B．边长为l的正方形金属框abcd（下简称方框）放在光滑的水平地面上，其外侧套着一个与方框边长相同的U形金属框架MNPQ（下简称U形框），U形框与方框之间接触良好且无摩擦．两个金属框每条边的质量均为m，每条边的电阻均为r．
如图甲所示，空间存在着以x=0平面为理想分界面的两个匀强磁场，左右两边磁场的磁感应强度分别为B1和B2，且B1：B2=4：3．方向如图，现在原点O处有一静止的中性粒子，突然分裂成两个带电粒子a和b，已知a带正电荷，分裂时初速度方向沿x轴正方向．若a粒子在第4次经过y轴时，恰与b粒子相遇．（1）在图乙中，画出a粒子的运动轨迹及用字母c标出a、b两粒子相遇的位置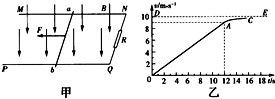
如图甲所示，空间存在B=0.5T、方向竖直向下的匀强磁场，MN、PQ是相互平行的粗糙的长直导轨，它们处于同一水平面内，其间距L=0.2m，R是连在导轨一端的电阻，ab是跨接在导轨上质量m=0.1kg的导体棒，从零时刻开始，通过一小型电动机对ab棒施加一个牵引力F，方向水平向左，使其从静止开始沿导轨做直线运动，此过程中棒始终保持与导轨垂直且接触良好，图乙是棒的速度一时间图象，其中OA段是直线，AC段是曲线，DE是曲线图象的渐近线，小型电动机在12s末达到额定功率P=4.5W，此后功率保持不变．导体棒和导轨的电阻均不计，g取10m/s2．