题目内容
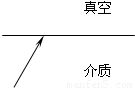
如图所示，一细光束从某种介质射向真空，该光束中含有频率分别为f1、f2的两种光．介质对这两种光的折射率分别为n1、n2，且n1＞n2．则：①两种光在介质中的速度之比v1：v2=
②两种光在介质中的波长之比λ1：λ2
③调整光的入射角度，使频率为f1的光在真空中刚好消失，此时频率为f2的光折射角的正弦值为 ．
【答案】分析：通过v=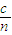
、
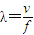以及折射定律求出光在介质中的速度之比、波长之比，以及求出频率为f2的光折射角的正弦值．
解答：解：①根据v=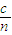
得，两种光在介质中的速度之比v1：v2=
．
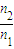②根据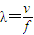
，
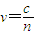得，
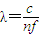，则两种光在介质中的波长之比λ1：λ2=
．
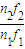③根据全反射的规律有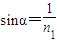
，通过折射定律得，
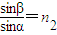，解得sinβ=
．
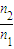故答案为：①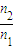
；②
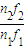；③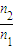
．
点评：解决本题的关键掌握光的折射定律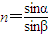
以及n=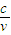
．
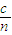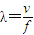、以及折射定律求出光在介质中的速度之比、波长之比，以及求出频率为f2的光折射角的正弦值．解答：解：①根据v=
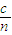得，两种光在介质中的速度之比v1：v2=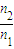．②根据
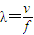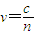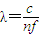，得，，则两种光在介质中的波长之比λ1：λ2=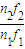．③根据全反射的规律有
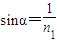，通过折射定律得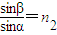，，解得sinβ=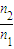．故答案为：①
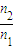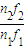；②；③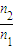．点评：解决本题的关键掌握光的折射定律
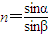以及n=．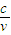 
练习册系列答案
相关题目
如图所示，一细光束从某种介质射向真空，该光束中含有频率分别为f1、f2的两种光．介质对这两种光的折射率分别为n1、n2，且n1＞n2．则：（8分）【物理－物理3-4】（将结果直接填在题目中的横线上）
（1）（4分）下列说法正确的是
| A．简谐运动的周期与振幅无关 |
B．在简谐运动的回复力表达式 中， 为振动物体受到的合外力， 为弹簧的劲度系数 |
| C．在波传播方向上，某个质点的振动速度就是波的传播速度 |
| D．在双缝干涉实验中，如果用紫光作为光源，遮住其中一条狭缝，屏上将呈现间距不等的明暗条纹 |
①两种光在介质中的速度之比
︰
②两种光在介质中的波长之比
︰
③调整光的入射角度，使频率为f1的光在真空中刚好消失，此时频率为f2的光折射角的正弦值为 。
中，
为振动物体受到的合外力，
为弹簧的劲度系数
︰
︰
中，
为振动物体受到的合外力，
为弹簧的劲度系数
①两种光在介质中的速度之比
︰
︰