题目内容
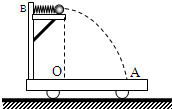 如图所示,水平光滑的桌面上放一质量为M的玩具小车,在小车的光滑的平台上有一质量可忽略的弹簧,弹簧的一端固定在平台上的B点,另一端接触质量为m的小球.若小车固定在桌面上,压缩弹簧,克服弹簧的弹力做功W时,将小球用细线拴住,然后烧断细线,小球被弹出,落在车上的A点.若小车不固定,压缩弹簧后用细线拴住小球,当小车和小球都静止时,烧断细线,将小球弹出.问:要想使小球也落到A点.压缩弹簧时,需克服弹簧弹力做多少功?(设弹簧压缩量远小于OA距离)
如图所示,水平光滑的桌面上放一质量为M的玩具小车,在小车的光滑的平台上有一质量可忽略的弹簧,弹簧的一端固定在平台上的B点,另一端接触质量为m的小球.若小车固定在桌面上,压缩弹簧,克服弹簧的弹力做功W时,将小球用细线拴住,然后烧断细线,小球被弹出,落在车上的A点.若小车不固定,压缩弹簧后用细线拴住小球,当小车和小球都静止时,烧断细线,将小球弹出.问:要想使小球也落到A点.压缩弹簧时,需克服弹簧弹力做多少功?(设弹簧压缩量远小于OA距离)分析:小车固定在桌面上时,小球离开平台后做平抛运动,由平抛运动知识可以求出小球的初速度,由动能定理得到W与小球平抛运动的高度和水平距离的关系;
小车不固定时,车与球组成的系统动量守恒,小球向右弹出后小车向左运动,由动量守恒定律、机械能守恒定律、平抛运动知识再得到弹簧弹性势能与小球平抛运动的高度和水平距离的关系;再联立,即可求解.
小车不固定时,车与球组成的系统动量守恒,小球向右弹出后小车向左运动,由动量守恒定律、机械能守恒定律、平抛运动知识再得到弹簧弹性势能与小球平抛运动的高度和水平距离的关系;再联立,即可求解.
解答:解:若小车固定,弹簧被压缩时具有弹性势能为:Ep=W.
根据小球和弹簧组成的系统机械能守恒得:Ep=
m
.
小球以v0作平抛运动,则有:
S0A=v0t
h=
gt2
联立以上四式,得:W=
若小车不固定,在水平方向上,小球和弹簧组成的系统动量守恒,则有:
m
=MV
系统的机械能守恒,则有:
Ep′=
m
+
MV2
小球以
作平抛运动,相对车的水平位移也为SOA,则有:
SOA=(
+V)t
由功能关系有:Ep′=W′
解以上各式得压缩弹簧需克服弹力做功为:
W′=
W
答:压缩弹簧时,需克服弹簧弹力做功为
W
根据小球和弹簧组成的系统机械能守恒得:Ep=
| 1 |
| 2 |
| v | 2 0 |
小球以v0作平抛运动,则有:
S0A=v0t
h=
| 1 |
| 2 |
联立以上四式,得:W=
m
| ||
| 8h |
若小车不固定,在水平方向上,小球和弹簧组成的系统动量守恒,则有:
m
| v | ′ 0 |
系统的机械能守恒,则有:
Ep′=
| 1 |
| 2 |
| v′ | 2 0 |
| 1 |
| 2 |
小球以
| v | ′ 0 |
SOA=(
| V | ′ 0 |
由功能关系有:Ep′=W′
解以上各式得压缩弹簧需克服弹力做功为:
W′=
| M |
| M+m |
答:压缩弹簧时,需克服弹簧弹力做功为
| M |
| M+m |
点评:本题涉及两种情形,根据机械能守恒、平抛运动和动量守恒定律得到克服弹簧弹力做功与平抛运动的高度、水平位移的关系是解题,考查综合应用力学知识的能力.

练习册系列答案
相关题目
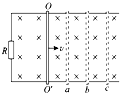 如图所示,水平光滑的平行金属导轨左端接有电阻R,匀强磁场方向竖直向下,质量一定的金属棒OO'垂直于导轨放置,现使棒以一定的初速度v向右运动,当金属棒通过位置a、b时速度分别是va、vb,到位置c时刚好静止,导轨和金属棒的电阻不计,ab=bc,则金属棒在由a到b和由b到c的两个过程中( )
如图所示,水平光滑的平行金属导轨左端接有电阻R,匀强磁场方向竖直向下,质量一定的金属棒OO'垂直于导轨放置,现使棒以一定的初速度v向右运动,当金属棒通过位置a、b时速度分别是va、vb,到位置c时刚好静止,导轨和金属棒的电阻不计,ab=bc,则金属棒在由a到b和由b到c的两个过程中( )| A、金属棒的加速度相等 | B、通过电阻R的电荷量相等 | C、电阻R上产生的焦耳热相等 | D、速度变化量相等 |
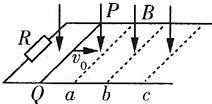 如图所示,水平光滑的平行金属导轨,左端接有电阻R,匀强磁场B竖直向下分布在导轨所在的空间内,质量一定的金属棒PQ垂直导轨放置.若使棒以一定能初速度v0向右运动,当其通过位置a、b时,速率分别为va、vb,到位置c时棒刚好静止,设金属导轨与棒的电阻均不计,a到b与b到c的间距相等,则金属棒在从a到b和从b到c的两个过程中( )
如图所示,水平光滑的平行金属导轨,左端接有电阻R,匀强磁场B竖直向下分布在导轨所在的空间内,质量一定的金属棒PQ垂直导轨放置.若使棒以一定能初速度v0向右运动,当其通过位置a、b时,速率分别为va、vb,到位置c时棒刚好静止,设金属导轨与棒的电阻均不计,a到b与b到c的间距相等,则金属棒在从a到b和从b到c的两个过程中( )| A、回路中产生的内能相等 | B、棒运动的加速度相等 | C、安培力做功相等 | D、通过棒横截面积的电荷量相等 |
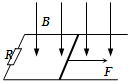 如图所示,水平光滑的金属框架上左端连接一个电阻R,有一金属杆在外力F的作用下沿框架向右由静止开始做匀加速直线运动,匀强磁场方向竖直向下,轨道与金属杆的电阻不计并接触良好,则能反映R中的感应电流I和外力F随时间t变化规律的图象是( )
如图所示,水平光滑的金属框架上左端连接一个电阻R,有一金属杆在外力F的作用下沿框架向右由静止开始做匀加速直线运动,匀强磁场方向竖直向下,轨道与金属杆的电阻不计并接触良好,则能反映R中的感应电流I和外力F随时间t变化规律的图象是( )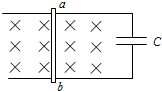 如图所示,水平光滑的U型金属框架中串入一个电容器,整个框架处于竖直向下的匀强磁场中,横跨在框架上的金属棒ab在外力的作用下,以速度v向右运动一段距离后突然停止运动.金属棒停止后,撤去外力作用,导轨足够长,则此后金属棒的运动情况是( )
如图所示,水平光滑的U型金属框架中串入一个电容器,整个框架处于竖直向下的匀强磁场中,横跨在框架上的金属棒ab在外力的作用下,以速度v向右运动一段距离后突然停止运动.金属棒停止后,撤去外力作用,导轨足够长,则此后金属棒的运动情况是( )