Question

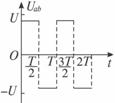
真空中足够大的两个相互平行的金属板a和b之间的距离为d，两板之间的电压Uab按图所示规律变化，其变化周期为T．在t=0时刻，一带电粒子（+q）仅在该电场的作用下，由a板从静止开始向b板运动，并于t=nT（n为自然数）时刻，恰好到达b板．试求：
（1）带电粒子运动过程中的最大速度为多少？
（2）若粒子在t=

T

6

时刻才开始从a板运动，那么经过同样长的时间，它将运动到离a板多远的地方？

Answer 1

分析：（1）带电粒子在两板之间电压Uab按图所示规律变化的电场中受到电场力作用，从而做匀变速运动．当a板从静止开始向b板运动，前半周期加速，后半周期减速，并于t=nT（n为自然数）时刻，恰好到达b板．
（2）则当t=

T

6

时刻才开始从a板运动，那么经过同样长的时间，前一段时间是先匀加速后匀减速，后一段时间回头匀加速，所以两段时间内的位移之差即为粒子离开a板的距离．由此可知最后一个周期尚未结束就已碰到b板．

解答：解：（1）带电粒子在匀强电场中的加速度为a，前半个周期为加速运动，后半个周期为减速运动，在一个周期中最后速度为0，带电粒子重复这个过程．所以在前半个周期末的速度最大．
     d=2n

1

2

a(

T

2

)2
     得到：a=

4d

nT2

    v=a

T

2

=

2d

nT2

（2）若粒子在t=

T

6

时刻开始从A板运动，该粒子向B板运动的距离：x1=2n

1

2

a(

2T

6

)2；
在电场力作用下返回，向A板运动的距离：x2=d=2n

1

2

a(

T

6

)2
该粒子向B板运动的总位移：x=2n[

1

2

a(

2

6

T)2-

1

2

a(

1

6

T)2]
联立以上公式，解得：x=

1

3

d
答：（1）带电粒子运动过程中的最大速度

2d

nT2

；（2）粒子将运动到离a板

d

3

的地方．

点评：由于粒子不是在电场中一直处于加速或减速，所以导致分析运动较复杂．同时也要注意到运动的周期性．