题目内容
正方形导线框处于匀强磁场中,磁场方向垂直框平面,磁感应强度随时间均匀增加,变化率为k.导体框质量为m、边长为L,总电阻为R,在恒定外力F作用下由静止开始运动.导体框在磁场中的加速度大小为 ,导体框中感应电流做功的功率为 .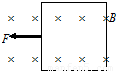
【答案】分析:对导线框受力分析,利用牛顿第二定律可以求出加速度;根据法拉第电磁感应定律可以求出感应电动势,再根据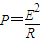 可以求出导体框中感应电流做功的功率.
可以求出导体框中感应电流做功的功率.
解答:解:导线框在磁场中受到的合外力等于F,由牛顿第二定律得:
导体框在磁场中的加速度大小为: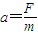
由法拉第地磁感应定律得:
线框中产生感应电动势为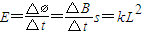
由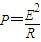 可得:
可得:
导体框中感应电流做功的功率为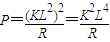
故答案为: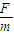
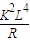
点评:解决此类问题的关键是熟练掌握感应电流产生条件,楞次定律,及法拉第电磁感应定律.
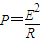 可以求出导体框中感应电流做功的功率.
可以求出导体框中感应电流做功的功率.解答:解:导线框在磁场中受到的合外力等于F,由牛顿第二定律得:
导体框在磁场中的加速度大小为:
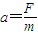
由法拉第地磁感应定律得:
线框中产生感应电动势为
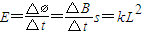
由
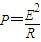 可得:
可得:导体框中感应电流做功的功率为
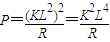
故答案为:
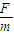
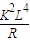
点评:解决此类问题的关键是熟练掌握感应电流产生条件,楞次定律,及法拉第电磁感应定律.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 (2012?上海)正方形导线框处于匀强磁场中,磁场方向垂直框平面,磁感应强度随时间均匀增加,变化率为k.导体框质量为m、边长为L,总电阻为R,在恒定外力F作用下由静止开始运动.导体框在磁场中的加速度大小为
(2012?上海)正方形导线框处于匀强磁场中,磁场方向垂直框平面,磁感应强度随时间均匀增加,变化率为k.导体框质量为m、边长为L,总电阻为R,在恒定外力F作用下由静止开始运动.导体框在磁场中的加速度大小为


