题目内容
（2012?上海）正方形导线框处于匀强磁场中，磁场方向垂直框平面，磁感应强度随时间均匀增加，变化率为k．导体框质量为m、边长为L，总电阻为R，在恒定外力F作用下由静止开始运动．导体框在磁场中的加速度大小为| F |
| m |
| F |
| m |
| K2L4 |
| R |
| K2L4 |
| R |
分析：对导线框受力分析，利用牛顿第二定律可以求出加速度；根据法拉第电磁感应定律可以求出感应电动势，再根据P=
可以求出导体框中感应电流做功的功率．
| E2 |
| R |
解答：解：导线框在磁场中受到的合外力等于F，由牛顿第二定律得：
导体框在磁场中的加速度大小为：a=
由法拉第的磁感应定律得：
线框中产生感应电动势为 E=
=
s=kL2
由P=
可得：
导体框中感应电流做功的功率为 P=
=
故答案为：
导体框在磁场中的加速度大小为：a=
| F |
| m |
由法拉第的磁感应定律得：
线框中产生感应电动势为 E=
| △? |
| △t |
| △B |
| △t |
由P=
| E2 |
| R |
导体框中感应电流做功的功率为 P=
| (KL2)2 |
| R |
| K2L4 |
| R |
故答案为：
| F |
| m |
| K2L4 |
| R |
点评：解决此类问题的关键是熟练掌握感应电流产生条件，楞次定律，及法拉第电磁感应定律．
练习册系列答案
相关题目
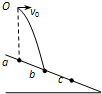（2012?上海）如图所示，斜面上a、b、c三点等距，小球从a点正上方O点抛出，做初速为v0的平抛运动，恰落在b点．若小球初速变为v，其落点位于c，则（ ）
（2012?上海模拟）如图所示，用三条细线悬挂的水平圆形线圈共有n匝，线圈由粗细均匀、单位长度的质量为2.5×10-3kg的导线绕制而成，三条细线呈对称分布，稳定时线圈平面水平．在线圈正下方放有一个圆柱形条形磁铁，磁铁的中轴线OO′垂直于线圈平面且通过其圆心O，测得线圈的导线所在处磁感应强度大小为0.5T，方向与竖直线成30°角，要使三条细线上的张力为零，线圈中通过的电流至少为（ ）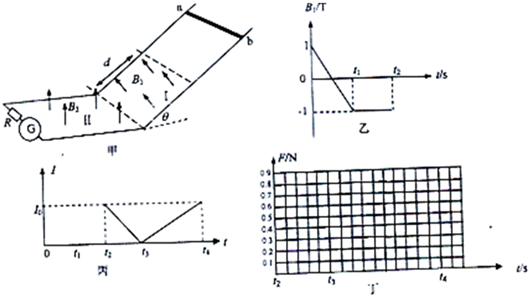
（2012?上海）载流长直导线周围磁场的磁感应强度大小为B=
（2012?上海）图a为测量分子速率分布的装置示意图．圆筒绕其中心匀速转动，侧面开有狭缝N，内侧贴有记录薄膜，M为正对狭缝的位置．从原子炉R中射出的银原子蒸汽穿过屏上的S缝后进入狭缝N，在圆筒转动半个周期的时间内相继到达并沉积在薄膜上．展开的薄膜如图b所示，NP，PQ间距相等．则（ ）