题目内容
 (2009?烟台二模)一质量为m的滑块以初速度v0自固定在地面上的粗糙斜面的底端开始冲上斜面,到达某一高度后又自动返回至斜面底端,图中分别给出了在整个运动过程中滑块的速度v、加速度a、动能EK及重力势能EP随时间t的变化关系图线,则其中可能正确的是( )(规定斜面底端所在水平面为参考平面)
(2009?烟台二模)一质量为m的滑块以初速度v0自固定在地面上的粗糙斜面的底端开始冲上斜面,到达某一高度后又自动返回至斜面底端,图中分别给出了在整个运动过程中滑块的速度v、加速度a、动能EK及重力势能EP随时间t的变化关系图线,则其中可能正确的是( )(规定斜面底端所在水平面为参考平面)分析:根据牛顿第二定律求出上滑和下滑过程中的加速度大小,从而得出速度随时间的变化规律,根据动能定理得出动能与位移的规律,根据重力势能的减小量等于重力做功,得出重力势能与时间变化关系.
解答:解:A、上滑时的加速度a1=
=gsinθ+μgcosθ,下滑时的加速度a2=
=gsinθ-μgcosθ.知a1>a2.速度时间图线的斜率表示加速度,故A错误、B正确.
C、动能是标量,不存在负值.故C错误.
D、物块向上做匀减速直线运动,向下做匀加速直线运动,位移与时间成二次函数关系,重力做功等于重力势能的减小量,所以重力势能先增大后减小,随时间成二次函数关系变化.故D正确.
故选BD.
| mgsinθ+μmgcosθ |
| m |
| mgsinθ-μmgcosθ |
| m |
C、动能是标量,不存在负值.故C错误.
D、物块向上做匀减速直线运动,向下做匀加速直线运动,位移与时间成二次函数关系,重力做功等于重力势能的减小量,所以重力势能先增大后减小,随时间成二次函数关系变化.故D正确.
故选BD.
点评:解决本题的关键根据牛顿第二定律得出上滑和下滑的加速度,判断出物体的运动情况.

练习册系列答案
相关题目
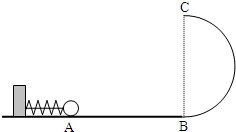 (2009?烟台二模)如图所示,竖直放置的光滑半圆形轨道与光滑水平面AB相切于B点,半圆形轨道的最高点为C.轻弹簧一端固定在竖直挡板上,另一端有一质量为0.1kg的小球(小球与弹簧不相连).用力将小球向左推,小球将弹簧压缩一定量时用细绳固定住.此时弹簧的弹性势能为4.05J.烧断细绳,弹簧将小球弹出.取g=10m/s2,求
(2009?烟台二模)如图所示,竖直放置的光滑半圆形轨道与光滑水平面AB相切于B点,半圆形轨道的最高点为C.轻弹簧一端固定在竖直挡板上,另一端有一质量为0.1kg的小球(小球与弹簧不相连).用力将小球向左推,小球将弹簧压缩一定量时用细绳固定住.此时弹簧的弹性势能为4.05J.烧断细绳,弹簧将小球弹出.取g=10m/s2,求