题目内容
一电荷量为q(q>0)、质量为m的带电粒子在匀强电场的作用下,在t=0时由静止开始运动,场强随时间变化的规律如图所示.不计重力,求在t=0到t=T的时间间隔内(1)粒子位移的大小和方向;
(2)粒子沿初始电场反方向运动的时间.
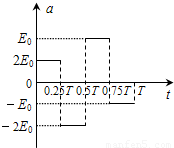
【答案】分析:(1)根据加速度与时间的关系,可确定速度与时间的关系,从而由面积等于位移的大小即可求解,并确定其方向;
(2)根据速度与时间的图象,来确定沿初始电场反方向运动的时间.
解答: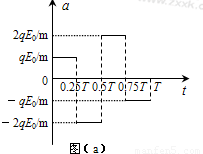
解:粒子在0~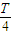 、
、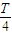 ~
~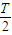 、
、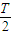 ~
~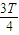 、
、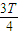 ~T时间间隔内做匀变速运动,
~T时间间隔内做匀变速运动,
设加速度分别为a1、a2、a3、a4,由牛顿第二定律得qE=ma1、2qE=-ma2、2qE=ma3、qE=-ma4
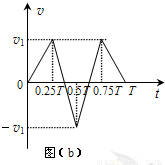
由此得带电粒子在0~T时间间隔内运动的a-t图象如图 (a)所示,对应的v-t图象如图(b)所示,其中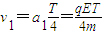
由图(b)可知,带电粒子在t=0到t=T时的位移为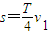
联立解得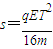
它的方向沿初始电场正方向.
(2)由图(b)可知,粒子在t=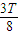 到t=
到t=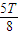 内沿初始电场反方向运动,
内沿初始电场反方向运动,
总的运动时间为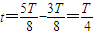
答:(1)粒子位移的大小为得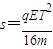 和方向沿初始电场正方向;
和方向沿初始电场正方向;
(2)粒子沿初始电场反方向运动的时间得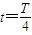 .
.
点评:另一种解法:(1)带电粒子在粒子在0~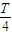 、
、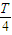 ~
~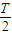 、
、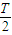 ~
~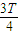 、
、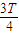 ~T时间间隔内做匀变速运动,设加速度分别为a1、a2、a3、a4,由牛顿第二定律得qE=ma1、2qE=-ma2、2qE=ma3、qE=-ma4
~T时间间隔内做匀变速运动,设加速度分别为a1、a2、a3、a4,由牛顿第二定律得qE=ma1、2qE=-ma2、2qE=ma3、qE=-ma4
设粒子在t=T/4、t=T/2、t=3T/4、t=T时刻的速度分别为v1、v2、v3、v4,则有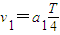 、
、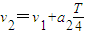 、
、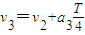 、
、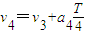
设带电粒子在t=0到t=T时的位移为s,有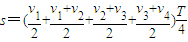
解得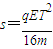
它的方向沿初始电场正方向.
(2)由电场的变化规律知,粒子从t=T/4时开始减速,设经过时间t1粒子速度为零,有0=v1+a2t1,解得 t1=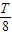
粒子从t=T/2时开始加速,设经过时间t2粒子速度为零,有0=v2+a3t2,解得 t2=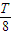
设粒子从t=0到t=T内沿初始电场反方向运动的时间为t2,有
t=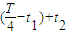
解得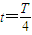
(2)根据速度与时间的图象,来确定沿初始电场反方向运动的时间.
解答:


解:粒子在0~
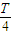 、
、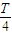 ~
~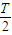 、
、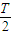 ~
~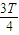 、
、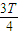 ~T时间间隔内做匀变速运动,
~T时间间隔内做匀变速运动,设加速度分别为a1、a2、a3、a4,由牛顿第二定律得qE=ma1、2qE=-ma2、2qE=ma3、qE=-ma4
由此得带电粒子在0~T时间间隔内运动的a-t图象如图 (a)所示,对应的v-t图象如图(b)所示,其中
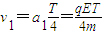
由图(b)可知,带电粒子在t=0到t=T时的位移为
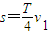
联立解得
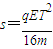
它的方向沿初始电场正方向.
(2)由图(b)可知,粒子在t=
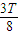 到t=
到t=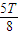 内沿初始电场反方向运动,
内沿初始电场反方向运动,总的运动时间为
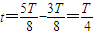
答:(1)粒子位移的大小为得
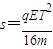 和方向沿初始电场正方向;
和方向沿初始电场正方向;(2)粒子沿初始电场反方向运动的时间得
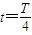 .
.点评:另一种解法:(1)带电粒子在粒子在0~
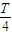 、
、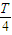 ~
~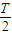 、
、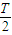 ~
~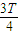 、
、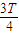 ~T时间间隔内做匀变速运动,设加速度分别为a1、a2、a3、a4,由牛顿第二定律得qE=ma1、2qE=-ma2、2qE=ma3、qE=-ma4
~T时间间隔内做匀变速运动,设加速度分别为a1、a2、a3、a4,由牛顿第二定律得qE=ma1、2qE=-ma2、2qE=ma3、qE=-ma4设粒子在t=T/4、t=T/2、t=3T/4、t=T时刻的速度分别为v1、v2、v3、v4,则有
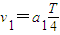 、
、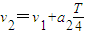 、
、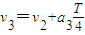 、
、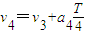
设带电粒子在t=0到t=T时的位移为s,有
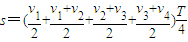
解得
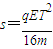
它的方向沿初始电场正方向.
(2)由电场的变化规律知,粒子从t=T/4时开始减速,设经过时间t1粒子速度为零,有0=v1+a2t1,解得 t1=
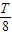
粒子从t=T/2时开始加速,设经过时间t2粒子速度为零,有0=v2+a3t2,解得 t2=
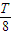
设粒子从t=0到t=T内沿初始电场反方向运动的时间为t2,有
t=
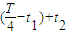
解得
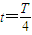

练习册系列答案
相关题目
 如图所示,一个内壁光滑的绝缘细直管竖直放置.在管子的底部固定一电荷量为Q(Q>0)的带电体.在距离底部点电荷为h2的管口A处,有一电荷量为q(q>0)、质量为m的小球自静止释放,在距离底部点电荷为h1的B处速度恰好为零.现让一个电荷量为q、质量为2m的小球仍在A处自静止释放,已知静电力常量为k,重力加速度为g,则该小球( )
如图所示,一个内壁光滑的绝缘细直管竖直放置.在管子的底部固定一电荷量为Q(Q>0)的带电体.在距离底部点电荷为h2的管口A处,有一电荷量为q(q>0)、质量为m的小球自静止释放,在距离底部点电荷为h1的B处速度恰好为零.现让一个电荷量为q、质量为2m的小球仍在A处自静止释放,已知静电力常量为k,重力加速度为g,则该小球( ) 如图所示,在由一个点电荷Q形成的电场中,有一条竖直的电场线,a、b、c为该电场线上的三点.一电荷量为q(q>0),质量为m的小球在a点由静止释放,运动到b点时速度达到最大,到c点时速度恰好为零,a、c间距离为h.则下列说法中正确的是( )
如图所示,在由一个点电荷Q形成的电场中,有一条竖直的电场线,a、b、c为该电场线上的三点.一电荷量为q(q>0),质量为m的小球在a点由静止释放,运动到b点时速度达到最大,到c点时速度恰好为零,a、c间距离为h.则下列说法中正确的是( )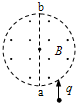 如图,半径为R的圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外.一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为R/2.已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( )
如图,半径为R的圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外.一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为R/2.已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( )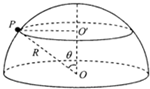 (2008?四川)如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上.整个空间存在匀强磁场,磁感应强度方向竖直向下.一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O′.球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ<
(2008?四川)如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上.整个空间存在匀强磁场,磁感应强度方向竖直向下.一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O′.球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ<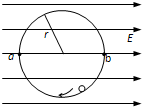 如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行.a、b为轨道直径的两端,该直径与电场方向平行.一电荷量为q(q>0)的质点沿轨道内侧运动,经过a点和b点时对轨道压力的大小分别为Na和Nb.不计重力,求:(1)电场强度的大小E;
如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行.a、b为轨道直径的两端,该直径与电场方向平行.一电荷量为q(q>0)的质点沿轨道内侧运动,经过a点和b点时对轨道压力的大小分别为Na和Nb.不计重力,求:(1)电场强度的大小E;