题目内容
11. 如图所示,质量分别为M1=0.48kg和M2=0.5kg的木块静置在光滑水平地面上,两木块间夹有一轻质弹簧,一粒质量m=0.02kg的弹丸以v0=150m/s的速度打入木块M1并停留在其中(打击时间极短),求:
如图所示,质量分别为M1=0.48kg和M2=0.5kg的木块静置在光滑水平地面上,两木块间夹有一轻质弹簧,一粒质量m=0.02kg的弹丸以v0=150m/s的速度打入木块M1并停留在其中(打击时间极短),求:①当弹丸在木块M1中相对静止的瞬间木块M1的速度v1;
②当M2的速度v=1m/s时弹簧的弹性势能Ep.
分析 ①弹丸打入木块M1的过程,两者构成的系统动量守恒,由动量守恒定律求当弹丸在木块M1中相对静止的瞬间木块M1的速度v1;
②弹丸停留在木块M1中一起压缩弹簧与M2作用过程中动量守恒,机械能也守恒.根据动量守恒定律和机械能守恒定律结合求M2的速度v=1m/s时弹簧的弹性势能Ep.
解答 解:①弹丸与木块M1作用过程中,以两者构成的系统为研究对象,取向右为正方向,由动量守恒定律得:
mv0=(m+M1)v1…①
代入数据解得:v1=6m/s…②
②弹丸停留在木块M1中一起压缩弹簧与M2作用过程中,弹丸、两木块组成的系统动量守恒,机械能也守恒,取向右为正方向,则得:
(m+M1)v1=(m+M1)v2+M2v…③
$\frac{1}{2}$(m+M1)v12=Ep+$\frac{1}{2}$(m+M1)v22+$\frac{1}{2}$M2v2…④
联解③④得:Ep=2.5J.…⑤
答:①当弹丸在木块M1中相对静止的瞬间木块M1的速度v1是6m/s.
②当M2的速度v=1m/s时弹簧的弹性势能Ep是2.5J.
点评 应用动量守恒定律时要清楚研究的对象和研究的过程;把动量守恒和能量守恒结合起来列出等式求解是常见的问题.本题要注意在弹丸打入M1的过程中,弹簧和M2没有参与.

练习册系列答案
相关题目
2. 如图,两电荷量分别为Q(Q>0)和-Q的点电荷对称地固定于x轴上的(x0,0)和(-x0,0),a点位于x轴上O点与点电荷-Q之间,b点位于y轴O点上方,坐标为(0,2x0)取无穷远处的电势为零.下列说法正确的是( )
如图,两电荷量分别为Q(Q>0)和-Q的点电荷对称地固定于x轴上的(x0,0)和(-x0,0),a点位于x轴上O点与点电荷-Q之间,b点位于y轴O点上方,坐标为(0,2x0)取无穷远处的电势为零.下列说法正确的是( )
 如图,两电荷量分别为Q(Q>0)和-Q的点电荷对称地固定于x轴上的(x0,0)和(-x0,0),a点位于x轴上O点与点电荷-Q之间,b点位于y轴O点上方,坐标为(0,2x0)取无穷远处的电势为零.下列说法正确的是( )
如图,两电荷量分别为Q(Q>0)和-Q的点电荷对称地固定于x轴上的(x0,0)和(-x0,0),a点位于x轴上O点与点电荷-Q之间,b点位于y轴O点上方,坐标为(0,2x0)取无穷远处的电势为零.下列说法正确的是( )| A. | b点电势为零,电场强度也为零 | |
| B. | 正试探电荷在a点的电势能大于零 | |
| C. | 将正的试探电荷从O点沿y轴移到b点,电场力先减小后增大 | |
| D. | 将负试探电荷放于b点时所受电场力方向沿x轴正方向 |
6. 如图所示,S是水面波的波源,MN是挡板,S1、S2是两个狭缝.已知两狭缝的宽度相等且比波长小得多,狭缝的开合可以控制.下列判断正确的是( )
如图所示,S是水面波的波源,MN是挡板,S1、S2是两个狭缝.已知两狭缝的宽度相等且比波长小得多,狭缝的开合可以控制.下列判断正确的是( )
 如图所示,S是水面波的波源,MN是挡板,S1、S2是两个狭缝.已知两狭缝的宽度相等且比波长小得多,狭缝的开合可以控制.下列判断正确的是( )
如图所示,S是水面波的波源,MN是挡板,S1、S2是两个狭缝.已知两狭缝的宽度相等且比波长小得多,狭缝的开合可以控制.下列判断正确的是( )| A. | 若合上S1,只打开S2,则会看到水波隐定的干涉图样 | |
| B. | 若合上S1,只打开S2,则会看到水波的衍射现象 | |
| C. | 若S1、S2都打开,则会看到水波隐定的干涉图样 | |
| D. | 若S1、S2都打开,则会看到水波的衍射现象 |
16.若卫星质量为m、离地球表面的高度为h,地球质量为M、半径为R,G为引力常量,则地球对卫星万有引力的大小为( )
| A. | $\frac{GMm}{{R}^{2}}$ | B. | $\frac{GMm}{(R+h)^{2}}$ | C. | $\frac{GMm}{(R+h)}$ | D. | $\frac{GMm}{{h}^{2}}$ |
3.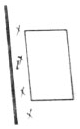 如图所示,矩形线圈位于通电长直导线附近,线圈与导线在同一平面内,通电直导线中电流i与时间t的关系有图A、B、C、D四种情况,在0~t0这段时间内,矩形线圈中有方向不变的感应电流的是( )
如图所示,矩形线圈位于通电长直导线附近,线圈与导线在同一平面内,通电直导线中电流i与时间t的关系有图A、B、C、D四种情况,在0~t0这段时间内,矩形线圈中有方向不变的感应电流的是( )
 如图所示,矩形线圈位于通电长直导线附近,线圈与导线在同一平面内,通电直导线中电流i与时间t的关系有图A、B、C、D四种情况,在0~t0这段时间内,矩形线圈中有方向不变的感应电流的是( )
如图所示,矩形线圈位于通电长直导线附近,线圈与导线在同一平面内,通电直导线中电流i与时间t的关系有图A、B、C、D四种情况,在0~t0这段时间内,矩形线圈中有方向不变的感应电流的是( )| A. | 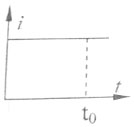 | B. | 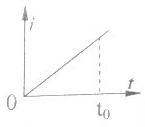 | C. |  | D. |  |
20. 如图所示,一木块静置于光滑的水平面上,一颗子弹沿水平方向射入木块,若子弹进入木块的深度为x2,与此同时木块沿水平面移动了x1.设子弹在木块中受到的阻力大小不变,则在子弹进入木块的过程中( )
如图所示,一木块静置于光滑的水平面上,一颗子弹沿水平方向射入木块,若子弹进入木块的深度为x2,与此同时木块沿水平面移动了x1.设子弹在木块中受到的阻力大小不变,则在子弹进入木块的过程中( )
 如图所示,一木块静置于光滑的水平面上,一颗子弹沿水平方向射入木块,若子弹进入木块的深度为x2,与此同时木块沿水平面移动了x1.设子弹在木块中受到的阻力大小不变,则在子弹进入木块的过程中( )
如图所示,一木块静置于光滑的水平面上,一颗子弹沿水平方向射入木块,若子弹进入木块的深度为x2,与此同时木块沿水平面移动了x1.设子弹在木块中受到的阻力大小不变,则在子弹进入木块的过程中( )| A. | 子弹损失的动能与木块获得的动能之比为(x1+x2):x1 | |
| B. | 子弹损失的动能与系统产生的内能之比为(x1+x2):x1 | |
| C. | 木块获得的动能与系统产生的内能之比为x1:x2 | |
| D. | 木块获得的动能与系统产生的内能之比为x2:x1 |
1.科学家使用核反应获取氚,再利用氘和氚核反应获得能量,核反应方程分别为:X+Y→${\;}_{2}^{4}$He+${\;}_{1}^{3}$H+4.9MeV和${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+X+17.6MeV,下列表述正确的有( )
| A. | X是质子 | B. | Y的质子数是3,中子数是6 | ||
| C. | 两个核反应都没有质量亏损 | D. | 氘和氚的核反应是核聚变反应 |
