题目内容
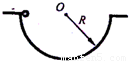
如图所示,半径为R光滑半圆形轨道固定在竖直平面内,质量为m的小球(可视为质点)从图示位置无初速释放,求:(1)小球通过轨道最低点时的速度大小;
(2)小球通过轨道最低点时对轨道的压力大小.
【答案】分析:(1)根据机械能守恒定律分别求出小球通过最低点时的速度大小.
(2)小球经过最低点时,由重力和支持力的合力提供向心力,根据牛顿运动定律求解小球对轨道压力的大小.
解答:解:(1)设小球通过轨道最低点时的速度大小为v.以轨道最低点所在的水平面为参考平面,根据机械能守恒定律得:
mgR=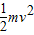 ,得到v=
,得到v=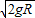
(2)以小球为研究对象,根据牛顿第二定律得:
N-mg=m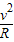
解得,N=3mg
由牛顿第三定律得:小球通过轨道最低点时对轨道的压力大小N′=N=3mg
答:
(1)小球通过轨道最低点时的速度大小是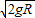 ;
;
(2)小球通过轨道最低点时对轨道的压力大小是3mg.
点评:本题是机械能守恒定律与向心力知识的综合应用,小球通过最低点时的加速度、轨道的支持力与半径无关是经验结论,要在理解的基础上记住.
(2)小球经过最低点时,由重力和支持力的合力提供向心力,根据牛顿运动定律求解小球对轨道压力的大小.
解答:解:(1)设小球通过轨道最低点时的速度大小为v.以轨道最低点所在的水平面为参考平面,根据机械能守恒定律得:
mgR=
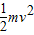 ,得到v=
,得到v=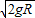
(2)以小球为研究对象,根据牛顿第二定律得:
N-mg=m
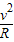
解得,N=3mg
由牛顿第三定律得:小球通过轨道最低点时对轨道的压力大小N′=N=3mg
答:
(1)小球通过轨道最低点时的速度大小是
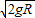 ;
;(2)小球通过轨道最低点时对轨道的压力大小是3mg.
点评:本题是机械能守恒定律与向心力知识的综合应用,小球通过最低点时的加速度、轨道的支持力与半径无关是经验结论,要在理解的基础上记住.

练习册系列答案
相关题目
 如图所示,半径为R的半圆柱形玻璃砖,放置在直角坐标系xOy中,圆心与坐标系原点O重合.在第二象限中坐标为(-1.5R,
如图所示,半径为R的半圆柱形玻璃砖,放置在直角坐标系xOy中,圆心与坐标系原点O重合.在第二象限中坐标为(-1.5R, (2010?武汉二模)如图所示,半径为R的圆形偏振片P的透振方向为竖直方向,一束横截面半径略小于R的平行自然光正对着偏振片P照射后射到屏上,现以光的传播方向OO′为轴将偏振片P旋转90°,则在偏振片P旋转的过程中( )
(2010?武汉二模)如图所示,半径为R的圆形偏振片P的透振方向为竖直方向,一束横截面半径略小于R的平行自然光正对着偏振片P照射后射到屏上,现以光的传播方向OO′为轴将偏振片P旋转90°,则在偏振片P旋转的过程中( )

 r处有一点光源S,已知水的折射率n=
r处有一点光源S,已知水的折射率n= .
.