Question

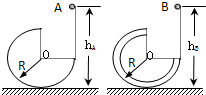如图所示，两个

3

4

圆弧轨道固定在水平地面上，半径R相同，A轨道由金属凹槽制成，B轨道由金属圆管制成，均可视为光滑轨道．在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放，小球距离地面的高度分别用h_A和h_B表示，则下列说法正确的是（　　）

A．若h_A=h_B=R，则两小球都能上升到离地高度为R的位置

B．若h_A=h_B=2R，则两小球在轨道最低点对轨道的压力为4mg

C．适当调整h_A和h_B，均可使两小球从轨道最高点飞出后，恰好落在轨道右端口处

D．若使小球沿轨道运动并且能从最高点飞出，A小球的最小高度为5R/2，B小球在h_B＞2R的任何高度均可

Answer 1

分析：小球A恰好能到A轨道的最高点时，轨道对小球无作用力，由重力提供小球的向心力，由牛顿第二定律求出速度．小球恰好能到B轨道的最高点时，速度为零，根据机械能守恒分别求出h_A和h_B．再判断h_A=h_B=2R，两小球是否能沿轨道运动到最高点．根据最高点的临界速度求出小球最高点飞出的水平位移的最小值．

解答：解：A、若h_A=h_B=R，根据机械能守恒定律可知，两小球都到达与O点等高的位置速度为零，即两小球都能上升到离地高度为R的位置，故A正确；
B、若h_A=h_B=2R，根据机械能守恒定律可知

1

2

mvA2=mg?2R，所以A在最低点的速度为vA=

2g×2R

=2

gR

，在最低点有：N-mg=m

vA2

R

，解得：N=5mg，同理可求B球在最低点对轨道的压力为5mg，故B错误；
C、小球A从最高点飞出后下落R高度时，水平位移的最小值为：x_A=vA

2R g

=

gR

2R g

=

2

R＞R，小球A落在轨道右端口外侧．而适当调整h_B，B可以落在轨道右端口处．故C错误；
D、小球A恰好能到A轨道的最高点时，由mg=m

vA2

R

，vA=

gR

根据机械能守恒定律得，mg（h_A-2R）=

1

2

mvA2
解得：h_A=

5

2

R
小球恰好能到B轨道的最高点时，临界速度为零，根据机械能守恒定律得：
mg（h_B-2R）=0
若使小球沿轨道运动并且从最高点飞出，B小球h_B＞2R的任意高度释放都可以．故D正确．
故选AD

点评：本题是向心力、机械能守恒定律、平抛运动的综合，A轨道与轻绳系的球模型相似，B轨道与轻杆固定的球模型相似，要注意临界条件的不同．