题目内容
12.利用引力常量G和下列某一组数据,不能计算出地球质量的是( )| A. | 地球的半径及重力加速度(不考虑地球自转) | |
| B. | 人造卫星在地面附近绕地球做圆周运动的速度及周期 | |
| C. | 月球绕地球做圆周运动的周期及月球与地球间的距离 | |
| D. | 地球绕太阳做圆周运动的周期及地球与太阳间的距离 |
分析 万有引力为:F=$\frac{GMm}{{r}^{2}}$;向心力的表达式:F=$\frac{m{v}^{2}}{r}$=$\frac{m4{π}^{2}r}{{T}^{2}}$
解答 解:A、根据万有引力等于重力$\frac{GMm}{{r}^{2}}$=mg,可以计算出地球的质量,A正确;
B、根据v=$\frac{2πr}{T}$可计算出卫星的轨道半径r,万有引力提供向心力,则$\frac{GMm}{{r}^{2}}$=$\frac{m4{π}^{2}r}{{T}^{2}}$可求出地球质量,B正确;
C、根据$\frac{GMm}{{r}^{2}}$=$\frac{m4{π}^{2}r}{{T}^{2}}$可求出地球的质量,C正确;
D、可根据则$\frac{GMm}{{r}^{2}}$=$\frac{m4{π}^{2}r}{{T}^{2}}$计算出太阳的质量,但无法计算地球的质量,D错误.
本题问的是不能计算出地球质量的是,所以选D.
故选:D.
点评 本题考查万有引力和圆周运动的表达式,掌握常用的几个圆周运动公式,熟悉运用,问题就能迎刃而解.

练习册系列答案
相关题目
20. 如图所示,在水平板左端由一固定挡板,挡板上连接一轻质弹簧,紧贴弹簧放一质量为m的滑块,此时弹簧处于自然长度,已知滑块与板的动摩擦因数及最大静摩擦因数均为$\frac{{\sqrt{3}}}{3}$,现将板的右端缓慢抬起使板与水平面间的夹角为θ,最后直到板竖直,则有( )
如图所示,在水平板左端由一固定挡板,挡板上连接一轻质弹簧,紧贴弹簧放一质量为m的滑块,此时弹簧处于自然长度,已知滑块与板的动摩擦因数及最大静摩擦因数均为$\frac{{\sqrt{3}}}{3}$,现将板的右端缓慢抬起使板与水平面间的夹角为θ,最后直到板竖直,则有( )
 如图所示,在水平板左端由一固定挡板,挡板上连接一轻质弹簧,紧贴弹簧放一质量为m的滑块,此时弹簧处于自然长度,已知滑块与板的动摩擦因数及最大静摩擦因数均为$\frac{{\sqrt{3}}}{3}$,现将板的右端缓慢抬起使板与水平面间的夹角为θ,最后直到板竖直,则有( )
如图所示,在水平板左端由一固定挡板,挡板上连接一轻质弹簧,紧贴弹簧放一质量为m的滑块,此时弹簧处于自然长度,已知滑块与板的动摩擦因数及最大静摩擦因数均为$\frac{{\sqrt{3}}}{3}$,现将板的右端缓慢抬起使板与水平面间的夹角为θ,最后直到板竖直,则有( )| A. | 当0≤θ≤$\frac{π}{6}$时,弹簧的弹力始终为零 | |
| B. | 滑块与板之间的摩擦力随θ增大而减小 | |
| C. | 当θ=$\frac{π}{2}$时,弹簧的弹力等于滑块的重力 | |
| D. | 滑块与板之间的弹力先做正功后做负功 |
7.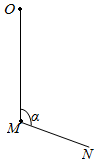 如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角α(α>$\frac{π}{2}$).现将重物向右上方缓慢拉起,并保持夹角α不变,在OM由竖直被拉到水平的过程中( )
如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角α(α>$\frac{π}{2}$).现将重物向右上方缓慢拉起,并保持夹角α不变,在OM由竖直被拉到水平的过程中( )
 如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角α(α>$\frac{π}{2}$).现将重物向右上方缓慢拉起,并保持夹角α不变,在OM由竖直被拉到水平的过程中( )
如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角α(α>$\frac{π}{2}$).现将重物向右上方缓慢拉起,并保持夹角α不变,在OM由竖直被拉到水平的过程中( )| A. | MN上的张力逐渐增大 | B. | MN上的张力先增大后减小 | ||
| C. | OM上的张力逐渐增大 | D. | OM上的张力先增大后减小 |
4. 如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻R.金属棒ab与两导轨垂直并保持良好接触,整个装置放在匀强磁场中,磁场方向垂直于导轨平面向下.现使磁感应强度随时间均匀减小,ab始终保持静止,下列说法正确的是( )
如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻R.金属棒ab与两导轨垂直并保持良好接触,整个装置放在匀强磁场中,磁场方向垂直于导轨平面向下.现使磁感应强度随时间均匀减小,ab始终保持静止,下列说法正确的是( )
 如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻R.金属棒ab与两导轨垂直并保持良好接触,整个装置放在匀强磁场中,磁场方向垂直于导轨平面向下.现使磁感应强度随时间均匀减小,ab始终保持静止,下列说法正确的是( )
如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻R.金属棒ab与两导轨垂直并保持良好接触,整个装置放在匀强磁场中,磁场方向垂直于导轨平面向下.现使磁感应强度随时间均匀减小,ab始终保持静止,下列说法正确的是( )| A. | ab中的感应电流方向由b到a | B. | ab中的感应电流逐渐减小 | ||
| C. | ab所受的安培力保持不变 | D. | ab所受的静摩擦力逐渐减小 |
7. 如图所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出滑块的Ek-h图象,其中高度从0.2m上升到0.35m范围内图象为直线,其余为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )
如图所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出滑块的Ek-h图象,其中高度从0.2m上升到0.35m范围内图象为直线,其余为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )
 如图所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出滑块的Ek-h图象,其中高度从0.2m上升到0.35m范围内图象为直线,其余为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )
如图所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地高度h并作出滑块的Ek-h图象,其中高度从0.2m上升到0.35m范围内图象为直线,其余为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )| A. | 小滑块的质量为0.2kg | |
| B. | 轻弹簧原长为0.1m | |
| C. | 弹簧最大弹性势能为0.32J | |
| D. | 小滑块的重力势能与弹簧的弹性势能总和最小为0.38J |
 如图所示,“
如图所示,“ ”型平行金属导轨LMN和OPQ分别固定,所构成的两个平面其中MNPQ水平光滑,LMOP倾斜粗糙、与水平面的夹角为θ.将两根电阻均为R、质量均为m的导体杆ab和cd,垂直放置在导轨上,cd杆刚好静止.现以MP连线为界,在水平导轨间施加竖直向上的匀强磁场B1,倾斜导轨间施加垂直斜面向上的匀强磁场B2,两个磁场的磁感应强度大小均为B,让ab杆在水平恒力作用下由静止开始向右运动.当cd杆再次刚要滑动时ab杆恰好运动了位移x达到最大速度,已知两导轨间距为L,重力加速度为g,最大静摩擦力等于滑动摩擦力,金属导轨的电阻不计.求:
”型平行金属导轨LMN和OPQ分别固定,所构成的两个平面其中MNPQ水平光滑,LMOP倾斜粗糙、与水平面的夹角为θ.将两根电阻均为R、质量均为m的导体杆ab和cd,垂直放置在导轨上,cd杆刚好静止.现以MP连线为界,在水平导轨间施加竖直向上的匀强磁场B1,倾斜导轨间施加垂直斜面向上的匀强磁场B2,两个磁场的磁感应强度大小均为B,让ab杆在水平恒力作用下由静止开始向右运动.当cd杆再次刚要滑动时ab杆恰好运动了位移x达到最大速度,已知两导轨间距为L,重力加速度为g,最大静摩擦力等于滑动摩擦力,金属导轨的电阻不计.求: 某探究小组做“验证力的平行四边形定则”实验,将画有坐标轴(横轴为x轴,纵轴为y轴,最小刻度表示1mm)的纸贴在桌面上,如图(a)所示.将橡皮筋的一端Q固定在y轴上的B点(位于图示部分除外),另一端P位于y轴上的A点时,橡皮筋处于原长.
某探究小组做“验证力的平行四边形定则”实验,将画有坐标轴(横轴为x轴,纵轴为y轴,最小刻度表示1mm)的纸贴在桌面上,如图(a)所示.将橡皮筋的一端Q固定在y轴上的B点(位于图示部分除外),另一端P位于y轴上的A点时,橡皮筋处于原长.