题目内容
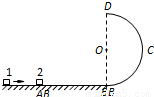
如图所示，水平光滑轨道AB与以O点为圆心的竖直半圆形光滑轨道BCD相切于B点，半圆形轨道的半径r=0.30m．在水平轨道上A点静置一质量为m2=0.12kg的物块2，现有一个质量m1=0.06kg的物块1以一定的速度向物块2运动，并与之发生正碰，碰撞过程中无机械能损失，碰撞后物块2的速度v2=4.0m/s．物块均可视为质点，g取10m/s2，求：（1）物块2运动到B点时对半圆形轨道的压力大小；
（2）发生碰撞前物块1的速度大小；
（3）若半圆形轨道的半径大小可调，则在题设条件下，为使物块2能通过半圆形轨道的最高点，其半径大小应满足什么条件．
【答案】分析：物体到达轨道B点对其受力分析，由牛顿第二定律可求出对轨道的压力．物体1与物体2碰撞，由动量守恒与机械能守恒定律可求出物体1碰撞前的速度．由物体2恰能通过最高点，再由机械能守恒定律可求出圆形轨道半径的极值．
解答：解：（1）设轨道B点对物块2的支持力为N，根据牛顿第二定律有
N-m2g=m2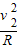
解得 N=7.6N
根据牛顿第三定律可知，物块2对轨道B点的压力大小N′=7.6N
（2）设物块1碰撞前的速度为v，碰撞后的速度为v1，对于物块1与物块2的碰撞过程，
根据动量守恒定律有 m1v=mv1+m2
因碰撞过程中无机械能损失，所以有
m1v2=
m1v12+
m2v22
代入数据联立解得 v=6.0m/s
（3）设物块2能通过半圆形轨道最高点的最大半径为Rm，对应的恰能通过最高点时的速度大小为v，根据牛顿第二定律，对物块2恰能通过最高点时有 m2g=m2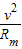
对物块2由B运动到D的过程，根据机械能守恒定律有
m2v22=m2g?2Rm+
m2v2
联立可解得：Rm=0.32m
所以，为使物块2能通过半圆形轨道的最高点，半圆形轨道半径不得大于0.32m．
点评：本题考查牛顿运动定律，运量守恒定律、机械能守恒定律，同时抓住物体2恰能通过最高点作为突破点入手研究．
解答：解：（1）设轨道B点对物块2的支持力为N，根据牛顿第二定律有
N-m2g=m2
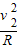
解得 N=7.6N
根据牛顿第三定律可知，物块2对轨道B点的压力大小N′=7.6N
（2）设物块1碰撞前的速度为v，碰撞后的速度为v1，对于物块1与物块2的碰撞过程，
根据动量守恒定律有 m1v=mv1+m2
因碰撞过程中无机械能损失，所以有
m1v2=m1v12+m2v22代入数据联立解得 v=6.0m/s
（3）设物块2能通过半圆形轨道最高点的最大半径为Rm，对应的恰能通过最高点时的速度大小为v，根据牛顿第二定律，对物块2恰能通过最高点时有 m2g=m2
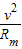
对物块2由B运动到D的过程，根据机械能守恒定律有
m2v22=m2g?2Rm+m2v2联立可解得：Rm=0.32m
所以，为使物块2能通过半圆形轨道的最高点，半圆形轨道半径不得大于0.32m．
点评：本题考查牛顿运动定律，运量守恒定律、机械能守恒定律，同时抓住物体2恰能通过最高点作为突破点入手研究．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图所示，一光滑的半径为R=0.5m的半圆形轨道固定在水平面上，一个质量为m的小球以某一速度从轨道最低点A处冲上轨道，当小球将要从轨道口B处水平飞出时，小球对轨道的压力恰好为4mg．最后小球落在地面C点．（g=10m/s2），小球落地点C距A点多远？
如图所示，一光滑的半径为R的半圆形轨道底部固定竖直放置在水平面上，一个质量为m的小球以某一速度冲上轨道，然后小球从轨道口B处飞出，最后落在水平面上，已知小球落地点C距B处的距离为3R．求：小球对轨道口B处的压力为多大？
如图所示，水平桌面上固定一个无电阻的光滑导轨，导轨左端由一个R=0.08Ω的电阻相连，轨距d=50cm．金属杆ab的质量m=0.1Kg，电阻r=0.02Ω，横跨导轨．磁感应强度B=0.2T的匀强磁场垂直穿过导轨平面．现用水平恒力F=0.1N拉ab从静止开始向右运动，求：
如图所示，平行光滑导轨MN、PQ相距L，电阻可忽略，其水平部分置于磁感应强度为B的竖直向上的匀强磁场中，导体棒a和b质量均为m，a棒电阻为R，b棒电阻为2R，a、b相距足够远，b放在水平导轨上，a从斜轨上高h处自由滑下．求
如图所示，一光滑的半径为R的半圆形轨道固定在水平面上，一个质量为m的小球以某一速度从轨道最低点A处冲上轨道，当小球将要从轨道口B处水平飞出时，小球对轨道的压力恰好为3mg．最后小球落在地面C点．