题目内容
（2005?西城区模拟）如图所示，车内绳AB与绳BC拴住一小球，BC水平，车由原来的静止状态变为向右加速直线运动，小球仍处于图中所示的位置，则（ ）分析：对小球受力分析，然后根据牛顿第二定律列式求解出两个拉力的表达式进行讨论．
解答：解：对球B受力分析，受重力、BC绳子的拉力FT2，AB绳子的拉力FT1，如图，根据牛顿第二定律，有
水平方向：FT2-FT1sinθ=ma
竖直方向：FT1cosθ-G=0
解得：FT1=
①
FT2=Gtanθ+ma ②
静止是加速度为零，故向右加速后，AB绳子的拉力不变，BC绳子的拉力变大；
故选D．
水平方向：FT2-FT1sinθ=ma
竖直方向：FT1cosθ-G=0
解得：FT1=
| G |
| cosθ |
FT2=Gtanθ+ma ②
静止是加速度为零，故向右加速后，AB绳子的拉力不变，BC绳子的拉力变大；
故选D．
点评：本题关键是对小球受力分析，根据牛顿第二定律列出方程求解出各个力的表达式，然后进行讨论．
练习册系列答案
相关题目
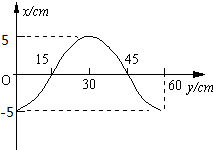（2005?西城区模拟）如图所示为波源O振动1.5s时沿波的传播方向上部分质点振动的波形图，已知波源O在t=0时开始沿x轴负方向振动，t=1.5s时它正好第二次到达波谷，问：
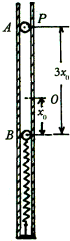（2005?西城区模拟）质量为m的小球B用一根轻质弹簧连接．现把它们放置在竖直固定的内壁光滑的直圆筒内，平衡时弹簧的压缩量为x0，如图所示，小球A从小球B的正上方距离为3x0的P处自由落下，落在小球B上立刻与小球B粘连在一起向下运动，它们到达最低点后又向上运动，并恰能回到0点（设两个小球直径相等，且远小于x0略小于直圆筒内径），已知弹簧的弹性势能为
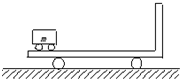（2005?西城区模拟）如图所示，质量为M=20kg的平板车静止在光滑的水平面上；车上最左端停放着质量为m=5kg的电动车，电动车与平板车上的挡板相距L=5m．电动车由静止开始向右做匀加速运动，经时间t=2s电动车与挡板相碰，问：