题目内容
 如图,在一光滑的水平面上,有三个质量都是m的物体,其中B、C静止,中间夹着一个质量不计的弹簧,弹簧处于松弛状态,今物体A以水平速度v0撞向B,且立即与其粘在一起运动.求整个运动过程中:
如图,在一光滑的水平面上,有三个质量都是m的物体,其中B、C静止,中间夹着一个质量不计的弹簧,弹簧处于松弛状态,今物体A以水平速度v0撞向B,且立即与其粘在一起运动.求整个运动过程中:(1)弹簧具有的最大弹性势能;
(2)物体C的最大速度.
分析:(1)A、B碰撞的瞬间动量守恒,求出碰撞后AB的共同速度,对ABC系统研究,抓住弹簧弹性势能相等时,三者速度相同,结合动量守恒定律求出共同的速度,根据机械能守恒定律求出弹簧具有的最大弹性势能.
(2)当弹簧压缩至最短再恢复原长时,C的速度最大,结合动量守恒定律和机械能守恒定律求出物体C的最大速度.
(2)当弹簧压缩至最短再恢复原长时,C的速度最大,结合动量守恒定律和机械能守恒定律求出物体C的最大速度.
解答:解:(1)A与B碰撞的过程中动量守恒,有mv0=2mv1
A与B碰后至弹簧压缩最短过程三物体系统动量守恒,根据动量守恒得
2mv1=3mv2
根据机械能守恒得,
?2mv12-
3mv22=Ep
联立解得Ep=
mv02.
(2)C物体的最大速度为v4,应在弹簧恢复原长时,由动量守恒定律得,
3mv2=2mv3+mv4
根据机械能守恒得:
?2mv12=
?2mv32+
mv42
联立两式解得v4=
.
答:(1)弹簧具有的最大弹性势能为
mv02.
(2)物体C的最大速度为
.
A与B碰后至弹簧压缩最短过程三物体系统动量守恒,根据动量守恒得
2mv1=3mv2
根据机械能守恒得,
| 1 |
| 2 |
| 1 |
| 2 |
联立解得Ep=
| 1 |
| 12 |
(2)C物体的最大速度为v4,应在弹簧恢复原长时,由动量守恒定律得,
3mv2=2mv3+mv4
根据机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
联立两式解得v4=
| 2v0 |
| 3 |
答:(1)弹簧具有的最大弹性势能为
| 1 |
| 12 |
(2)物体C的最大速度为
| 2v0 |
| 3 |
点评:本题考查了动量守恒定律和机械能守恒定律的综合运用,难度中等,运用动量守恒定律解题时关键确定好研究的系统.

练习册系列答案
相关题目
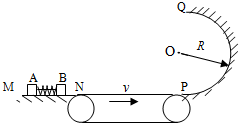 如图所示,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度L=0.8m,皮带以恒定速率v=3.0m/s向右匀速运动.传送带的右端处平滑连接着一个在竖直平面内、半径为R=0.4m的光滑半圆轨道PQ,两个质量均为m=0.2kg的滑块A、B置于水平导轨MN上,开始时滑块A、B之间用细绳相连,其间有一压缩的轻弹簧,系统处于静止状态.现使细绳断开,弹簧伸展,滑块B脱离弹簧后滑上传送带,从右端滑出并沿半圆轨道运动到最高点Q后水平飞出,又正好落回N点.已知滑块B与传送带之间的动摩擦因数μ=
如图所示,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度L=0.8m,皮带以恒定速率v=3.0m/s向右匀速运动.传送带的右端处平滑连接着一个在竖直平面内、半径为R=0.4m的光滑半圆轨道PQ,两个质量均为m=0.2kg的滑块A、B置于水平导轨MN上,开始时滑块A、B之间用细绳相连,其间有一压缩的轻弹簧,系统处于静止状态.现使细绳断开,弹簧伸展,滑块B脱离弹簧后滑上传送带,从右端滑出并沿半圆轨道运动到最高点Q后水平飞出,又正好落回N点.已知滑块B与传送带之间的动摩擦因数μ= (2013?郑州二模)如图所示,光滑的水平地面上有三块木块a、b、c,质量均为m,a、c之间用轻质细绳连接.现用一水平恒力F作用在b上,三者开始一起做匀加速运动.运动过程中把一块橡皮泥粘在某一木块上面,系统仍加速运动,且始终没有相对滑动.则在粘上橡皮泥并达到稳定后,下列说法正确的是( )
(2013?郑州二模)如图所示,光滑的水平地面上有三块木块a、b、c,质量均为m,a、c之间用轻质细绳连接.现用一水平恒力F作用在b上,三者开始一起做匀加速运动.运动过程中把一块橡皮泥粘在某一木块上面,系统仍加速运动,且始终没有相对滑动.则在粘上橡皮泥并达到稳定后,下列说法正确的是( ) 如图所示.光滑的水平面上有一个矩形导体框abcd,ab=0.4m,cd=0.6m,它的电阻为0.4Ω.它的右侧有一宽度为L=0.4m、磁感应强度为B=0.5T、方向竖直向下的匀强磁场.现用一外力将该导体框以大小为V=5.0m/S的速度匀速地拉到磁场的右侧.试求:
如图所示.光滑的水平面上有一个矩形导体框abcd,ab=0.4m,cd=0.6m,它的电阻为0.4Ω.它的右侧有一宽度为L=0.4m、磁感应强度为B=0.5T、方向竖直向下的匀强磁场.现用一外力将该导体框以大小为V=5.0m/S的速度匀速地拉到磁场的右侧.试求: