题目内容
2. 如图所示,均匀细杆AB质量为M,A端装有转轴,B端连接细线通过滑轮和质量为m的重物C相连,若杆AB呈水平,细线与水平方向夹角为θ 时恰能保持平衡,则下面表达式中正确的是( )
如图所示,均匀细杆AB质量为M,A端装有转轴,B端连接细线通过滑轮和质量为m的重物C相连,若杆AB呈水平,细线与水平方向夹角为θ 时恰能保持平衡,则下面表达式中正确的是( )| A. | M=2msinθ | B. | 滑轮受到的压力为2mg | ||
| C. | 杆对轴A的作用力大小为mg | D. | 杆对轴A的作用力大小$\frac{Mg}{2sinθ}$ |
分析 先对C物体进行受力分析,由二力平衡得出绳子的拉力,然后对杆进行受力分析,由共点力的平衡即可求出杆的重力与绳子的拉力之间的关系.
解答 解:A、由题可知,C物体受到重力和绳子的拉力处于平衡状态,所以绳子的拉力与C物体的重力大小相等,为mg;
对杆AB进行受力分析如图,则:
设AB杆的长度为L,由图可知,杆的重力产生的力矩是顺时针方向的力矩,力臂的大小是$\frac{1}{2}$L;绳子的拉力产生的力矩是逆时针方向的力矩,力臂的大小是Lsinθ,过转轴的力不产生力矩,由力矩平衡得:$Mg•\frac{1}{2}L=mgLsinθ$
所以:M=2msinθ ①.故A正确;
B、由题图可知,两根绳子的拉力的方向之间有夹角,所以两根绳子的拉力的合力大小要小于2mg,即滑轮受到的压力小于2mg.故B错误;
C、由受力图可知,轴A对杆的作用力的方向的反向延长线一定过绳子的拉力的延长线与重力的作用线的交点,由于重力的作用线过杆的中点,所以可知力F与绳子的拉力与水平方向之间的夹角是相等的,并且力:Fcosθ=mgcosθ,所以F与绳子的拉力的大小也相等,即F=mg ②.则杆对轴A的作用力大小为mg.故C正确;
D、联立①②可得:F=$\frac{Mg}{2sinθ}$,所以杆对轴A的作用力大小也可以表达为$\frac{Mg}{2sinθ}$.故D正确.
故选:ACD
点评 该题同时考查共点力作用下物体的平衡与力矩平衡,解题的关键是正确画出杆的受力图,找出各个力的力臂,然后又力矩平衡条件即可解答.

练习册系列答案
相关题目
13.做平抛运动的物体,在水平方向通过的最大距离取决于( )
| A. | 物体的高度和所受重力 | B. | 物体所受的重力和初速度 | ||
| C. | 物体的高度和初速度 | D. | 物体所受的重力、高度和初速度 |
7.一个做简谐运动的质点,它的振幅是4cm,周期是0.4s.该质点从平衡位置开始经过0.5s后,位移的大小和所通过的路程分别为( )
| A. | 4cm,10cm | B. | 4cm,20cm | C. | 0,24cm | D. | 100cm,100cm |
14. 如图所示,一列向右传播的简谐波,波速大小为0.6m/s,P质点的横坐标为x=0.96m,从图中状态开始计时,求:
如图所示,一列向右传播的简谐波,波速大小为0.6m/s,P质点的横坐标为x=0.96m,从图中状态开始计时,求:
(1)P质点刚开始振动时,振动方向如何?
(2)经过多长时间,P质点第一次达到波谷?
 如图所示,一列向右传播的简谐波,波速大小为0.6m/s,P质点的横坐标为x=0.96m,从图中状态开始计时,求:
如图所示,一列向右传播的简谐波,波速大小为0.6m/s,P质点的横坐标为x=0.96m,从图中状态开始计时,求:(1)P质点刚开始振动时,振动方向如何?
(2)经过多长时间,P质点第一次达到波谷?
11.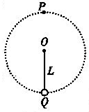 如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定轴O,杆可在竖直平面内绕轴O无摩擦转动,已知小球通过最高点P时,速度的大小为vP=$\sqrt{2gl}$,已知小球通过最低点Q时,速度的大小为vQ=$\sqrt{6gl}$,则小球的运动情况为( )
如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定轴O,杆可在竖直平面内绕轴O无摩擦转动,已知小球通过最高点P时,速度的大小为vP=$\sqrt{2gl}$,已知小球通过最低点Q时,速度的大小为vQ=$\sqrt{6gl}$,则小球的运动情况为( )
 如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定轴O,杆可在竖直平面内绕轴O无摩擦转动,已知小球通过最高点P时,速度的大小为vP=$\sqrt{2gl}$,已知小球通过最低点Q时,速度的大小为vQ=$\sqrt{6gl}$,则小球的运动情况为( )
如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定轴O,杆可在竖直平面内绕轴O无摩擦转动,已知小球通过最高点P时,速度的大小为vP=$\sqrt{2gl}$,已知小球通过最低点Q时,速度的大小为vQ=$\sqrt{6gl}$,则小球的运动情况为( )| A. | 小球到达圆周轨道的最高点P点受到轻杆向上的弹力 | |
| B. | 小球到达圆周轨道的最低点Q点受到轻杆向上的弹力 | |
| C. | 小球到达圆周轨道的最高点P,且在P点不受轻杆的作用力 | |
| D. | 若小球到达圆周轨道的最高点P速度增大,则P点受到轻杆向下的弹力增大 |
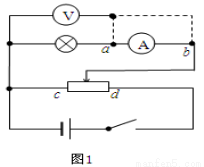
 某同学学习传感器后,用电源、电磁继电器、滑动变阻器、开关、导线等仪器设计了一个高温报警器,要求是:正常情况绿灯亮,有险情时电铃报警.电路如图所示,图中仪器还不完整,请完成以下问题:
某同学学习传感器后,用电源、电磁继电器、滑动变阻器、开关、导线等仪器设计了一个高温报警器,要求是:正常情况绿灯亮,有险情时电铃报警.电路如图所示,图中仪器还不完整,请完成以下问题: 有一种利用电磁分离同位素的装置,可以将某种化学元素的其它类型的同位素去除而达到浓缩该种特殊的同位素的目的,其工作原理如图所示.粒子源A产生的初速度为零、电荷量为e、质量为m的氕核和质量为2m氘核,经过电压为U0的加速电场加速后匀速通过准直管,从偏转电场的极板左端中央沿垂直电场方向射入匀强偏转电场,偏转后通过位于下极板中心位置的小孔S离开电场,进入范围足够大、上端和左端有理想边界、磁感应强度为B、方向垂直纸面向外的匀强磁场,磁场区域的上端以偏转电场的下极板为边界,磁场的左边界MN与偏转电场的下极板垂直,且MN与小孔S左边缘相交于M点.已知偏转极板的长度为其板间距离的2倍,整个装置处于真空中,粒子所受重力、小孔S的大小及偏转电场的边缘效应均可忽略不计.
有一种利用电磁分离同位素的装置,可以将某种化学元素的其它类型的同位素去除而达到浓缩该种特殊的同位素的目的,其工作原理如图所示.粒子源A产生的初速度为零、电荷量为e、质量为m的氕核和质量为2m氘核,经过电压为U0的加速电场加速后匀速通过准直管,从偏转电场的极板左端中央沿垂直电场方向射入匀强偏转电场,偏转后通过位于下极板中心位置的小孔S离开电场,进入范围足够大、上端和左端有理想边界、磁感应强度为B、方向垂直纸面向外的匀强磁场,磁场区域的上端以偏转电场的下极板为边界,磁场的左边界MN与偏转电场的下极板垂直,且MN与小孔S左边缘相交于M点.已知偏转极板的长度为其板间距离的2倍,整个装置处于真空中,粒子所受重力、小孔S的大小及偏转电场的边缘效应均可忽略不计. 如图所示,质量为M的平板小车放光滑水平面上,平板车右端上方放有质量为m的物体,它们之间的动摩擦因数为μ,现使平板车和物体分别向右和向左运动,初速度大小都是v0设平板小车足够长,且M>m,求物体相对平板小车右端滑行的距离.
如图所示,质量为M的平板小车放光滑水平面上,平板车右端上方放有质量为m的物体,它们之间的动摩擦因数为μ,现使平板车和物体分别向右和向左运动,初速度大小都是v0设平板小车足够长,且M>m,求物体相对平板小车右端滑行的距离.