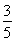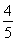题目内容
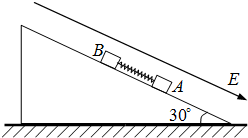 如图所示,有一固定的倾角为30°的斜面体,处在一个范围足够大的匀强电场中,电场线平行于斜面向下.斜面上放有两个物块A、B,质量分别为mA=0.8kg、mB=0.2kg,A带电,但B不带电,它们之间有一根用轻线拴住的压缩轻弹簧,弹簧与A相连,但与B不相连,弹簧的压缩量为30cm,具有的弹性势能为8.3J,A、B均处于静止状态.现突然剪断拴住弹簧的轻线,弹簧伸长并推动B沿斜面向上运动,直到B与弹簧分离,A、B在运动过程中始终没有离开斜面,一切摩擦都不计,并且A与斜面和弹簧的接触都是绝缘的,所带电荷量保持不变.(重力加速度g=10m/s2)
如图所示,有一固定的倾角为30°的斜面体,处在一个范围足够大的匀强电场中,电场线平行于斜面向下.斜面上放有两个物块A、B,质量分别为mA=0.8kg、mB=0.2kg,A带电,但B不带电,它们之间有一根用轻线拴住的压缩轻弹簧,弹簧与A相连,但与B不相连,弹簧的压缩量为30cm,具有的弹性势能为8.3J,A、B均处于静止状态.现突然剪断拴住弹簧的轻线,弹簧伸长并推动B沿斜面向上运动,直到B与弹簧分离,A、B在运动过程中始终没有离开斜面,一切摩擦都不计,并且A与斜面和弹簧的接触都是绝缘的,所带电荷量保持不变.(重力加速度g=10m/s2)(1)A带何种电荷?其所受电场力为多大?
(2)B从与弹簧分离到再次接触经历多长时间?
分析:(1)对A、B整体分析,根据共点力平衡得出A电荷的电性,以及电场力的大小.
(2)A、B系统重力沿斜面方向的分力等于电场力,知A、B系统所受的外力之和为零,系统动量守恒,根据动量守恒定律和能量守恒定律求出弹簧恢复原长时A、B的速度关系.根据牛顿第二定律分别求出B脱离弹簧后A、B的加速度,抓住两者的位移相等求出再次接触经历的时间.
(2)A、B系统重力沿斜面方向的分力等于电场力,知A、B系统所受的外力之和为零,系统动量守恒,根据动量守恒定律和能量守恒定律求出弹簧恢复原长时A、B的速度关系.根据牛顿第二定律分别求出B脱离弹簧后A、B的加速度,抓住两者的位移相等求出再次接触经历的时间.
解答:解:(1)由题意可知,A所受电场力应沿斜面向上,所以应带负电,
对整体分析,根据共点力平衡得,匀强电场力大小为:FE=(mA+mB)gsinθ=5N
(2)A、B组成的系统在沿斜面方向上动量守恒,根据动量守恒定律得,0=mAvA-mBvB
弹簧恢复原长时,A上滑的位移x1=
×30cm=6cm,B下滑的位移x2=
×30cm=24cm.
则A重力势能的增加量和B重力势能的减小量相等,
根据能量守恒得,Ep=
mAvA2+
mBvB2+qEx.
代入数据解得vA=2m/s,vB=6m/s.
弹簧恢复原长后,B的加速度aB=gsin30°=
g,方向沿斜面向下,A的加速度aA=
=
gsin30°=
g,方向沿斜面向上.
设经过t时间再次接触,则有:vBt-
aBt2=vAt-
aAt2
代入数据解得t=3.2s.
答:(1)A带负电,电场力为5N.
(2)B从与弹簧分离到再次接触经历的时间为3.2s.
对整体分析,根据共点力平衡得,匀强电场力大小为:FE=(mA+mB)gsinθ=5N
(2)A、B组成的系统在沿斜面方向上动量守恒,根据动量守恒定律得,0=mAvA-mBvB
弹簧恢复原长时,A上滑的位移x1=
| 1 |
| 5 |
| 4 |
| 5 |
则A重力势能的增加量和B重力势能的减小量相等,
根据能量守恒得,Ep=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得vA=2m/s,vB=6m/s.
弹簧恢复原长后,B的加速度aB=gsin30°=
| 1 |
| 2 |
| qE-mAgsinθ |
| mA |
| mB |
| mA |
| 1 |
| 8 |
设经过t时间再次接触,则有:vBt-
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得t=3.2s.
答:(1)A带负电,电场力为5N.
(2)B从与弹簧分离到再次接触经历的时间为3.2s.
点评:解决本题的关键知道A、B组成的系统在沿斜面方向所受的外力之和为零,动量守恒,结合动量守恒和能量守恒进行求解.

练习册系列答案
相关题目
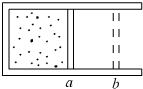 如图所示,有一固定的圆筒形绝热容器,用绝热活塞密封一定质量的气体,当活塞处于位置a时,筒内气体压强等于外界大气压,当活塞在外力作用下由位置a移动到位置b的过程中,下列说法正确的是( )
如图所示,有一固定的圆筒形绝热容器,用绝热活塞密封一定质量的气体,当活塞处于位置a时,筒内气体压强等于外界大气压,当活塞在外力作用下由位置a移动到位置b的过程中,下列说法正确的是( ) (2008?内江二模)如图所示.有一固定的圆筒形绝热容器,用绝热活塞密封了一定质量的气体(气体分子间相互作用的引力和斥力均忽略不计).当活塞处于位a时,筒内气体的压强等于外界的大气压强汽.当活塞在外力F的作用下由位置a移动到位置b的过程中,下列说法中正确的是( )
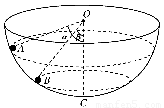
(2008?内江二模)如图所示.有一固定的圆筒形绝热容器,用绝热活塞密封了一定质量的气体(气体分子间相互作用的引力和斥力均忽略不计).当活塞处于位a时,筒内气体的压强等于外界的大气压强汽.当活塞在外力F的作用下由位置a移动到位置b的过程中,下列说法中正确的是( )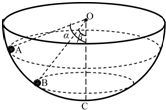 如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°,以最低点C所在的水平面为重力势能的参考平面,则(
如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°,以最低点C所在的水平面为重力势能的参考平面,则(