题目内容
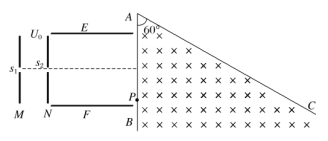
【题目】一重为G的吊桥由六根钢杆悬吊着，六根钢杆在桥面上分列两排，其上端挂在两根钢缆上，如图。已知图中相邻两钢杆间距离均为12m，靠桥面中心的钢杆长度AA′=DD′=3m，BB′=EE′，CC′=PP′，又已知两端钢缆与水平成45°角。钢杆自重不计。钢缆CF上的拉力大小为_____。为使每根钢杆承受负荷相同，钢杆BB′长度应为_____米。
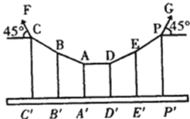
【答案】
7
【解析】
[1]．对整体受力分析，受重力和两个拉力F，根据平衡条件，有：
解得：
F=
[2]．对C点受力分析，受CC′杆的拉力、拉力F、BC钢缆的拉力，根据平衡条件，有：
水平方向：
Fcos45°=FBCcosθ1
（θ1为FBC与水平方向的夹角）
竖直方向：
Fsin45°=
+FBCsinθ1
解得：
tanθ1=
对B点受力分析，受BB′杆的拉力、BC钢索的拉力、AB钢索的拉力，根据平衡条件，有：
水平方向：
FBCcosθ1=FBAcosθ2
（θ2为FBA与水平方向的夹角）
竖直方向：
FBCsinθ1=+FBAsinθ2
解得：
tanθ2=
故
BB′=EE′=AA′+A′B′tanθ2=3+12×=7m
练习册系列答案
相关题目
