Question

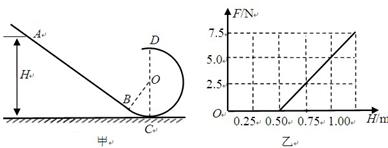
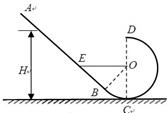
（12分）如图甲所示，竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成，AB和BCD相切于B点，CD连线是圆轨道竖直方向的直径（C、D为圆轨道的最低点和最高点），已知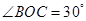。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下，用压力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F，并得到如图乙所示的压力F与高度H的关系图象，取g=10m/s²。求：

（1）滑块的质量和圆轨道的半径；

（2）是否存在某个H值，使得滑块经过最高点D后能直接落到直轨道AB上与圆心等高的点。若存在，请求出H值；若不存在，请说明理由。

 

Answer 1

【答案】

（1）m=0.1kg，R=0.2m（2）见解析

【解析】

试题分析：（1）mg(H－2R)= 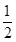mv_D²         2分

        F＋mg= 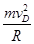                         2分

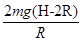得：F= －mg   

      m=0.1kg，R=0.2m                      2分

（2）假设滑块经过最高点D后能直接落到直轨道AB上与圆心等高的E点（如图所示）

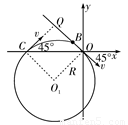
x= OE=v_DPt 1分

  R=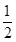gt²     1分                                                                                

得到：v_DP=2m/s             1分   

而滑块过D点的临界速度

v_DL=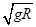=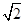m/s     1分

由于：v_DP> v_DL   所以存在一个H值，使得滑块经过最高点D后能直接落到直轨道AB上与圆心等高的点                                       1分

mg(H－2R)= 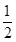mv_DP²        1分

得到：H=0.6m               1分

考点：考查了牛顿定律和圆周运动的综合应用

点评：做此类型题目的关键是找出临界条件，分清物体在各个过程中的运动性质，然后结合相对应的规律分析解题