题目内容
如图所示，回旋加速器的两个D型盒之间接有交变电源，电源电压为U．上方D 型盒中央为质子源，静止的质量为m电量为e的质子经电场加速后，进入下方的D型盒．其最大轨道半径 R，磁场的磁感应强度B，（1）质子最初进入下方D型盒的动能是
（2）质子经回旋加速器最后得到的动能是
（3）交变电源的周期是
分析：（1）根据质子在电场力作用下，被加速，由动能定理，即可求解；
（2）根据运动半径等于R，结合牛顿第二定律与向心力，即可求解；
（3）根据洛伦兹力提供向心力，即可求出运动的周期，从而确定交流电源的周期．
（2）根据运动半径等于R，结合牛顿第二定律与向心力，即可求解；
（3）根据洛伦兹力提供向心力，即可求出运动的周期，从而确定交流电源的周期．
解答：解：（1）质子在电场中被加速，根据动能定理，
则有最初进入下方D型盒的动能：Ek=eU；
（2）根据qvB=m
得，粒子出D形盒时的速度vm=
，则粒子出D形盒时的动能Ekm=
mv2=
；
（3）由洛伦兹力提供向心力，则有：Bqv=m
；
而T=
，所以粒子在磁场中运行周期为T=
；
因一直处于加速状态，则磁场中的周期与交流电源的周期相同，
即为：T=
；
故答案为：eU；
；
；
则有最初进入下方D型盒的动能：Ek=eU；
（2）根据qvB=m
| v2 |
| R |
| qBR |
| m |
| 1 |
| 2 |
| q2B2R2 |
| 2m |
（3）由洛伦兹力提供向心力，则有：Bqv=m
| v2 |
| r |
而T=
| 2πr |
| v |
| 2πm |
| eB |
因一直处于加速状态，则磁场中的周期与交流电源的周期相同，
即为：T=
| 2πm |
| eB |
故答案为：eU；
| q2B2R2 |
| 2m |
| 2πm |
| eB |
点评：考查粒子做匀速圆周的周期公式与半径公式的应用，掌握牛顿第二定律，注意交流电源变化周期与粒子在磁场中偏转周期的关系．
练习册系列答案
相关题目
（2006?南通二模）如图所示，回旋加速器是用来加速带电粒子使它获得很大动能的装置．其核心部分是两个D形金属盒，置于匀强磁场中，两盒分别与高频电源相连．则带电粒子加速所获得的最大动能与下列因素有关的（ ）
如图所示，回旋加速器是用来加速带电粒子使它获得很大动能的装置．其核心部分是两个“D”型金属盒，置于匀强磁场中，两盒分别与高频交流电源相连．则带电粒子获得的最大动能与下列哪些因素有关（ ）
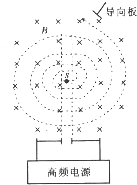如图所示为回旋加速器的原理示意图，其核心部分是两个D形盒，两盒分别和一高频交流电源的两极相连，高频电源的电压为U，匀强磁场垂直D形盒平面，磁感应强度为B，在D形盒中央s点处放有粒子源．当粒子源放出质量为m、带电量为q的粒子（设粒子的初速度为0），然后被回旋加速器加速，设D形盒的最大半径为R，则（ ）A、所加高频交流电的频率应是
| ||
B、所加高频交流电的频率应是
| ||
C、粒子离开加速器前被加速的次数为
| ||
D、粒子离开加速器时的动能是
|
如图所示，回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电源两极相连接的两个D形盒，两盒间构成一狭缝，两D形盒处于垂直于盒面的匀强磁场中．下列有关回旋加速器的描述正确的是（ ）
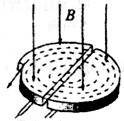如图所示，回旋加速器是用来加速带电粒子使它获得很大动能的装置．其核心部分是两个D型金属盒，置于匀强磁场中，两盒分别与高频电源相连．要求高频电源的周期与粒子在D型盒中运动周期相同．为增大某带电粒子加速后从D型盒边缘引出时的动能，下列措施可行的有（不考虑相对论效应）（ ）| A、减小磁感应强度．同时增大高频电源的周期 | B、增大磁感应强度，同时减小高频电源的周期 | C、增大磁感应强度，同时增大高频电源的电压 | D、减小高频电源的周期．同时增大高频电源的电压 |